Проецирование на кривые поверхности в Autodesk Inventor

Привет!

Сегодня новый видеоурок по Autodesk Inventor.

Научимся создавать ассиметричный ненаправленный рисунок протектора на тракторной шине.

Да, Вы правы. Этот урок, как и предыдущий, записал для вас Михаил Азанов. Подробнее о нем мы писали раньше.

Итак, урок «Проецирование на кривые поверхности в Autodesk Inventor».

Смотрим и не забываем оставлять комментарий.

Кстати, вот, что еще говорит Михаил:

Могу сделать урок с прекрасным механизмом Пафнутия Чебышева, русского математика девятнадцатого века — с так называемым «стопоходом» — прелесть, а не механизм…

Но интересен ли он Вам — я не знаю…

Если вам это интересно, или у вас есть какие-то мысли, то напишите в комментариях.

Удачи!

Проецирование на кривые поверхности в Autodesk Inventor

Невозможность выполнения операции рельеф на цилиндрическую и не на коническую, а именно на криволинейную поверхность, вынуждает идти на маленькие хитрости.

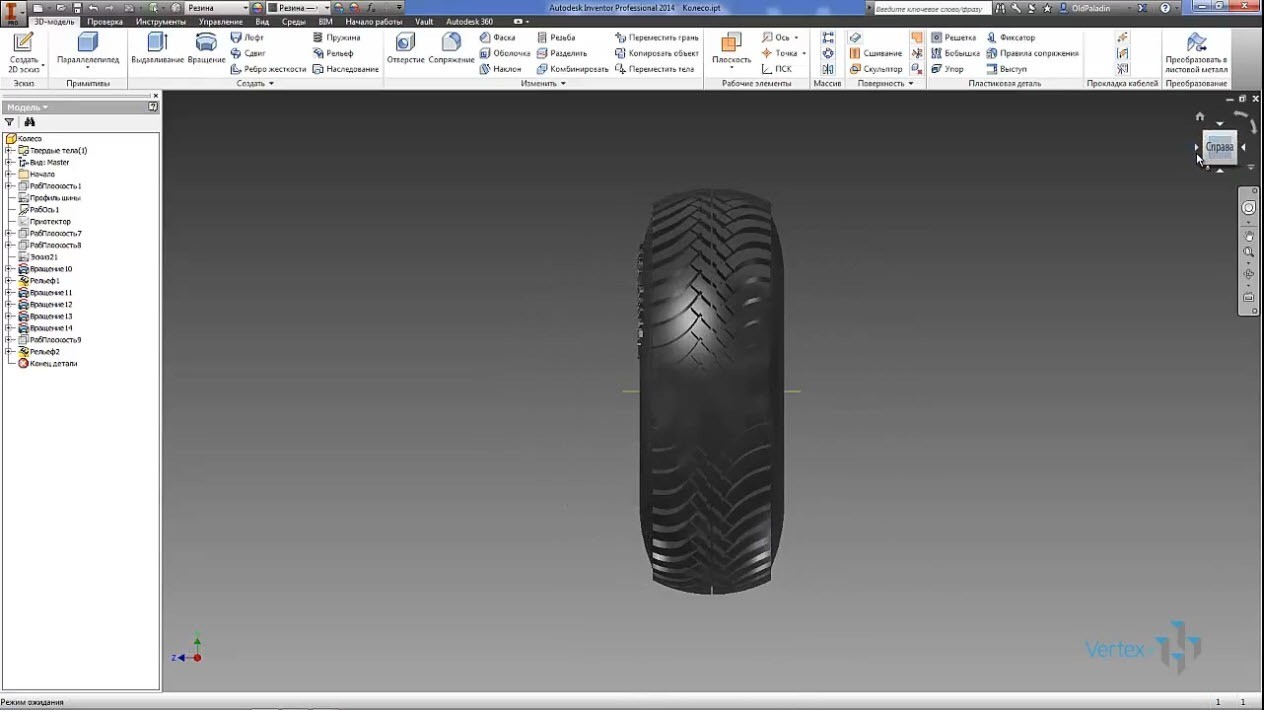
Попробуем создать автопокрышку со симметричным не направленным рисунком протектора достаточно близкому к реальному прототипу. Наглядно убедимся, что проецирование на цилиндрическую поверхность 3D эскиза мы ничего не достигаем.

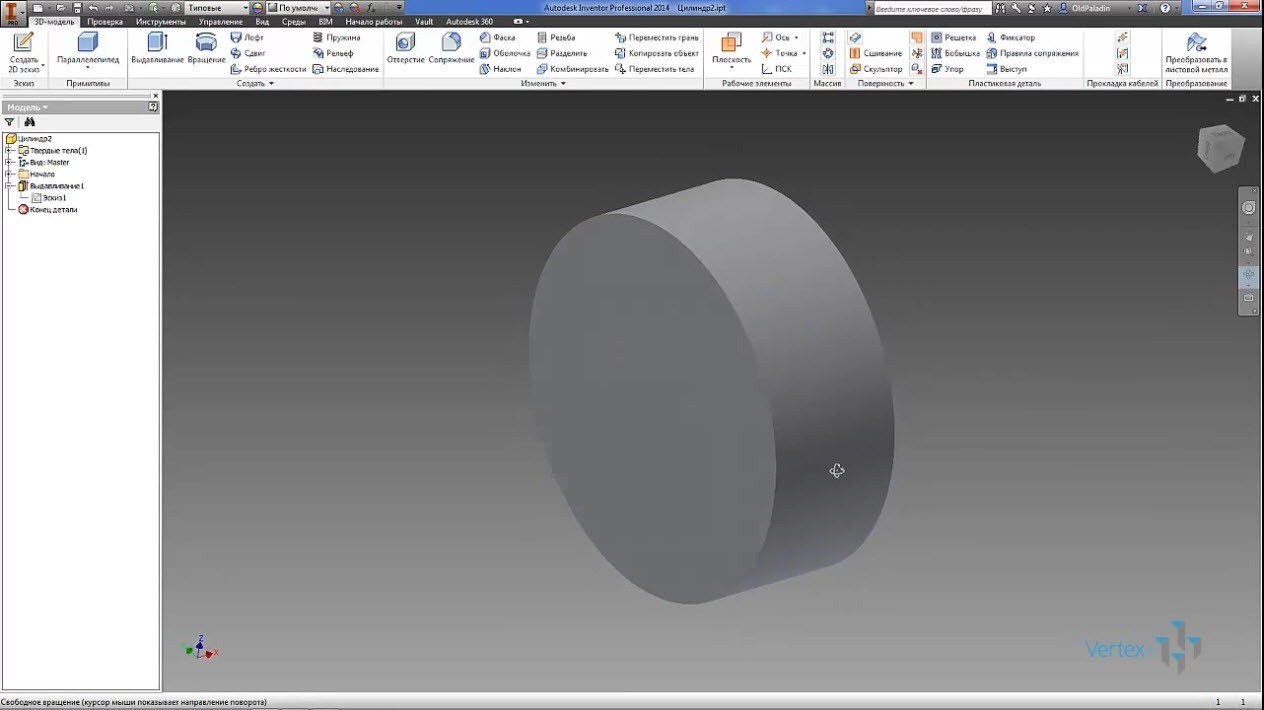
Создаем цилиндр близкий к размерам и пропорциям колеса автомобиля, а вместо протектора используем окружности. Элементарно рассчитаем число этих окружностей, чтобы они целое число раз уложились на развертке цилиндра.

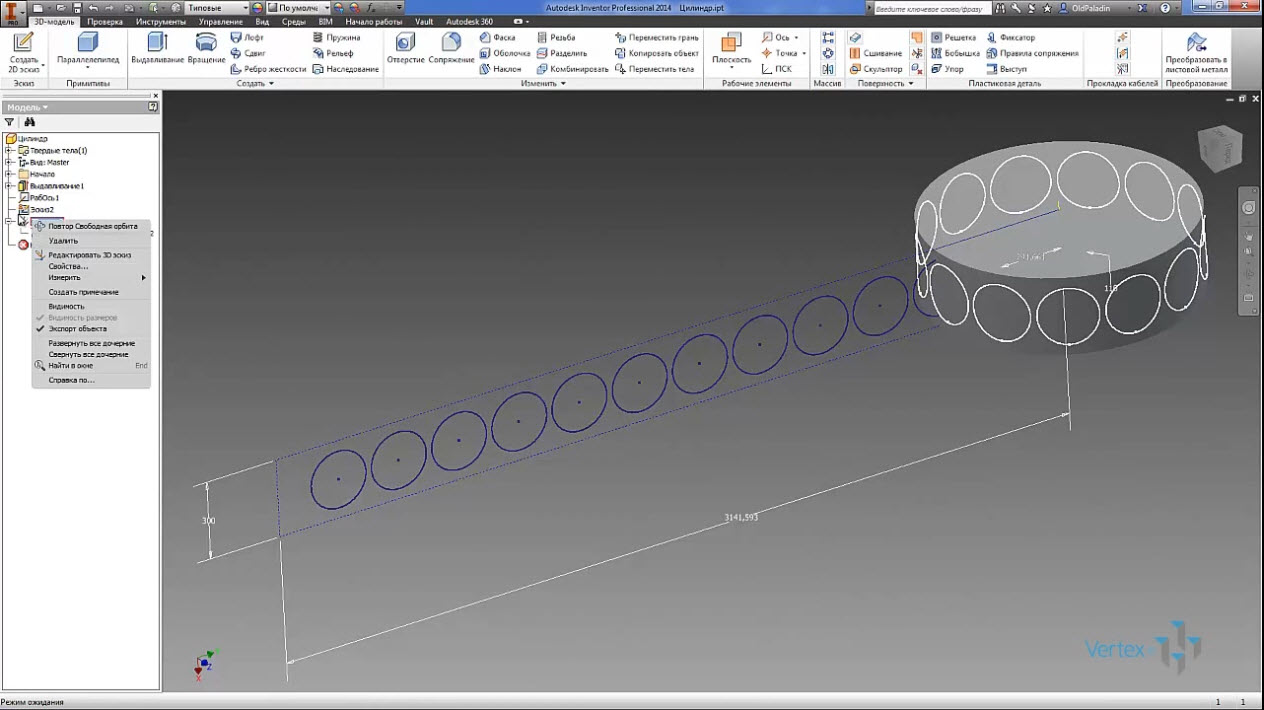
Создаем 2D эскиз в котором из окружности делаем прямоугольный массив с рассчитанным числом окружностей, а затем этот эскиз проецированием 3D эскиз размещаем эти окружности на цилиндрической поверхности.

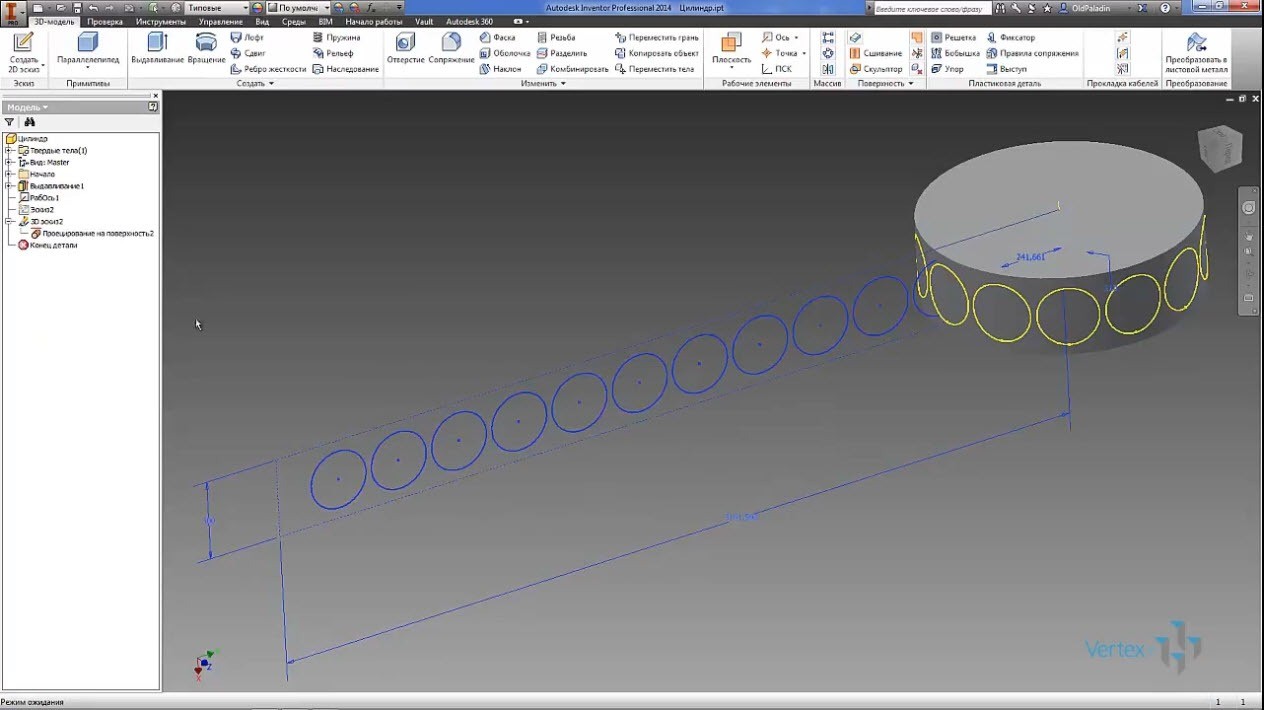
Ничего не добившись из проецированных фигур, выполняем операцию рельеф на ту же цилиндрическую поверхность.

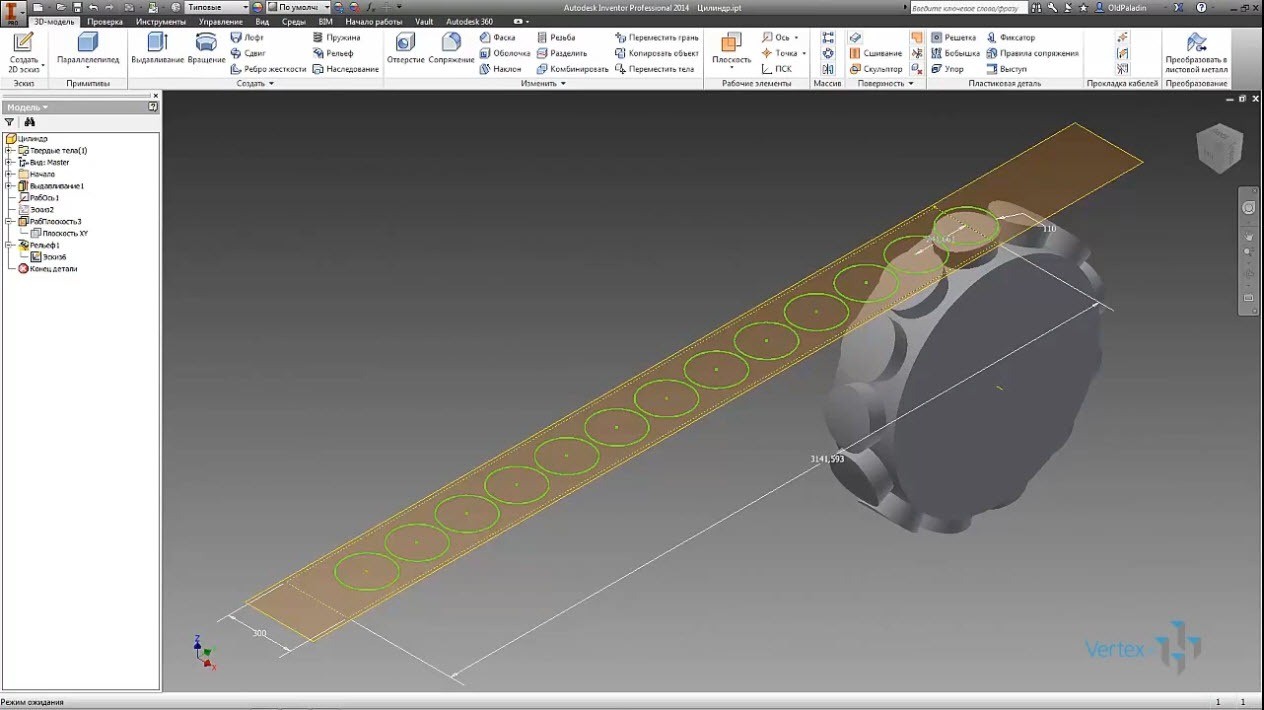
Теперь результат вдохновляет, и мы с воодушевлением строим эскизы с будущей покрышкой рисунка протектора. Воспользовавшись референсом из интернета.

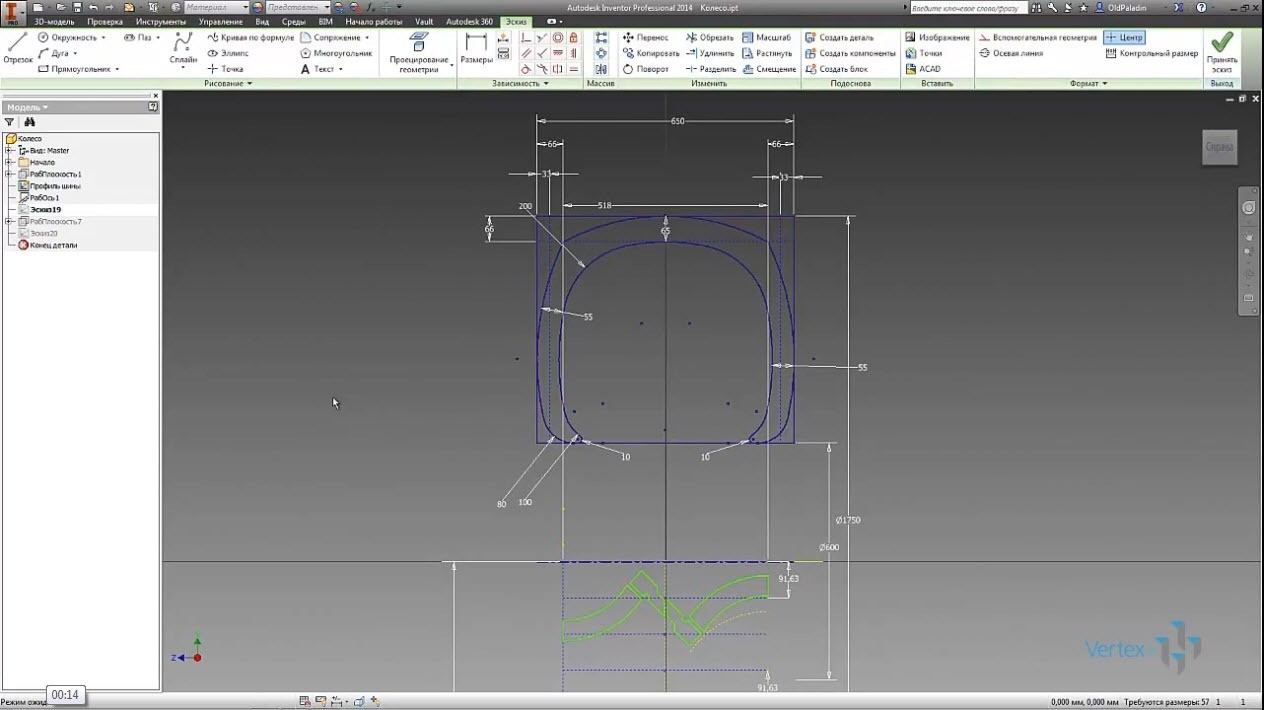
Заметьте, что эскиз профиля шины и эскиз рисунка протектора, это два разных эскиза.

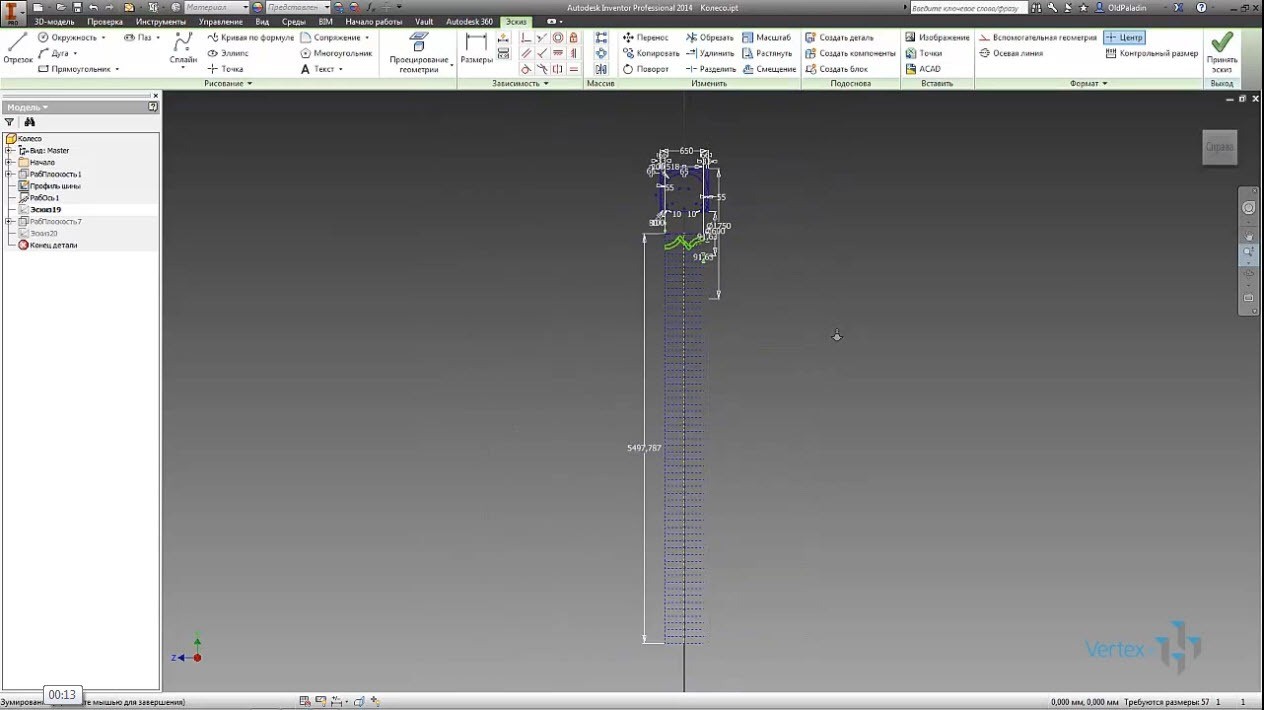
С использованием диаметра цилиндрической поверхности числа π и габаритов рисунка протектора определим число для прямоугольного массива с помощью которого сделаем полную развертку будущего протектора.

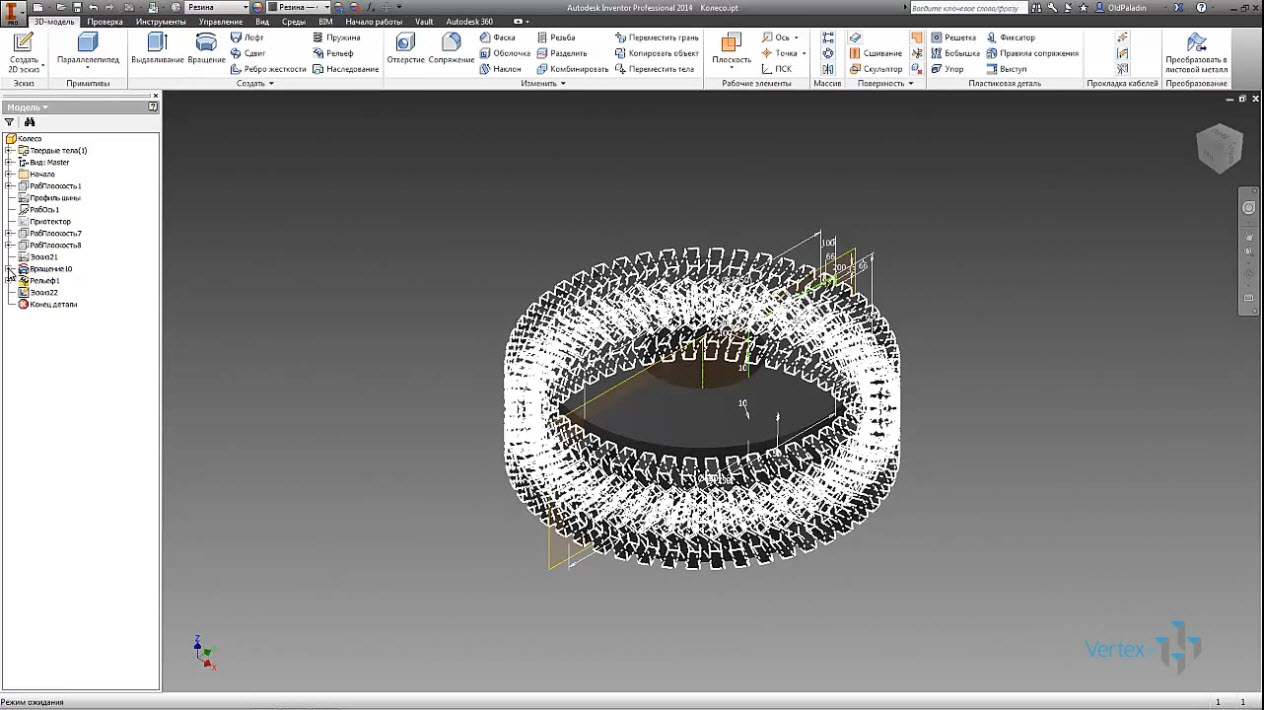
После проведения операции рельеф и появление на цилиндрической поверхности протектора, выдавленного с запасом по высоте рельефа и начинаются обещанные маленькие хитрости.

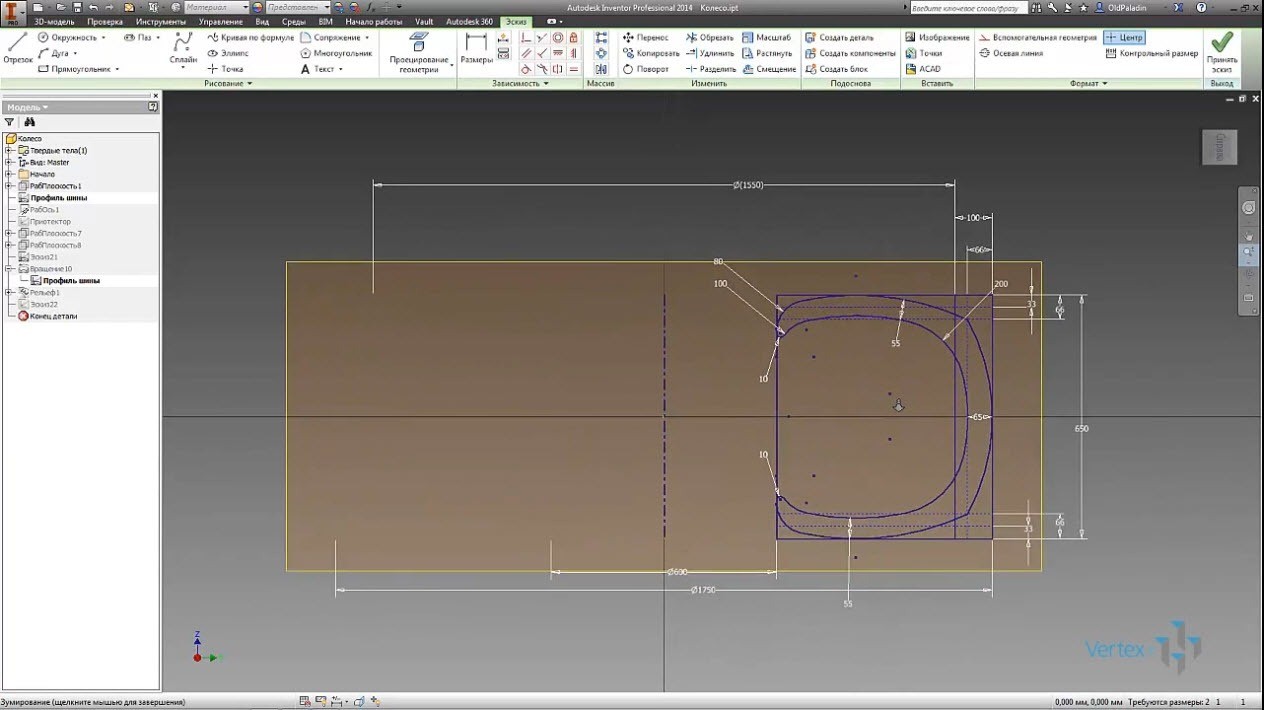
Самая большая хитрость заключается в многократном копировании эскиза профиля шины и манипулирование с его элементами. Делаем эскиз для формирование боковых поверхностей шины, удаляем не нужные элементы и добавляем к боковым линиям замыкающие линии.

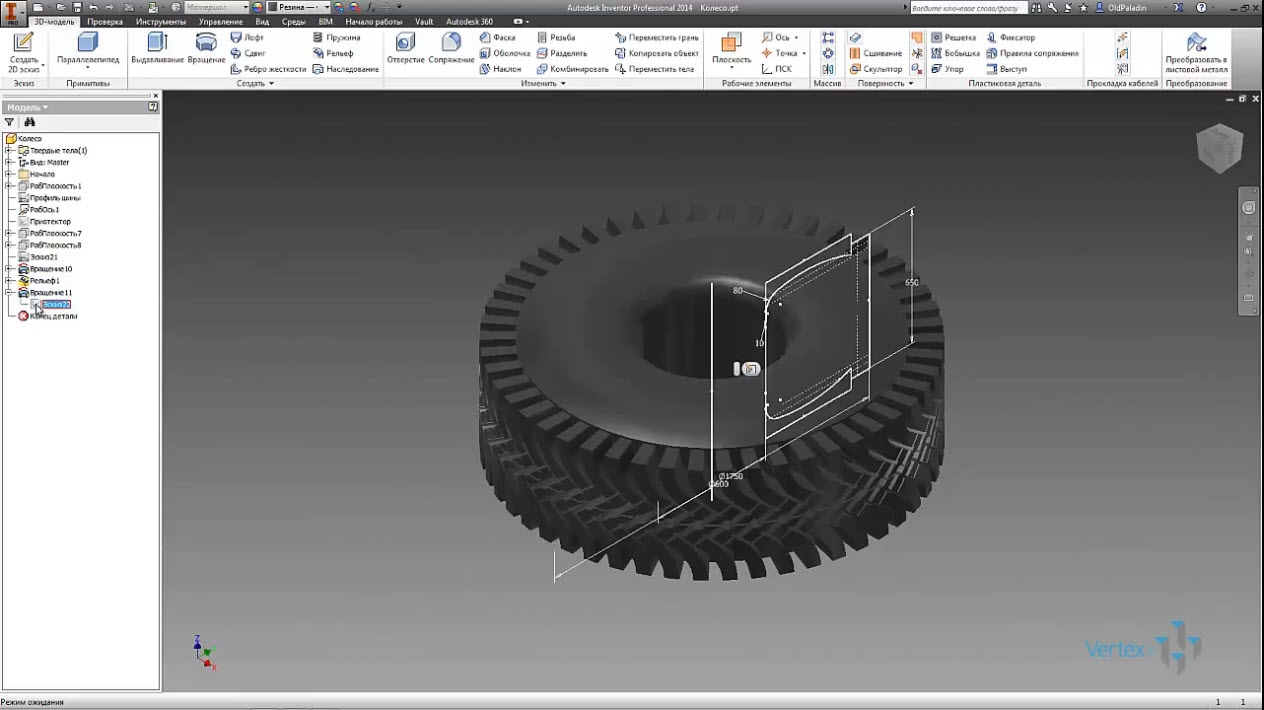
Операция вращения эскиза относительно оси покрышки, подрезаем бока в соответствие нашим идеальным представлениям о покрышкам.

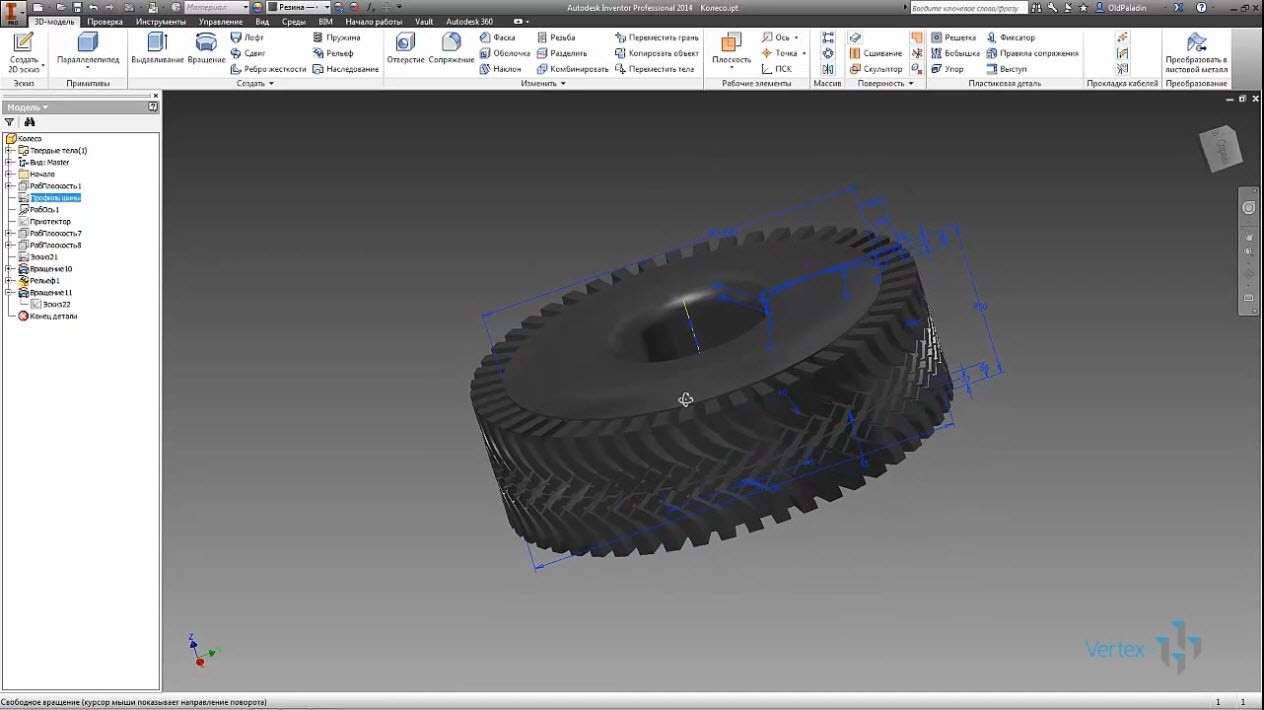
Оценим, полюбуемся. Благо, что есть возможность сделать поперечный разрез и прикинуть дальнейшие действия.

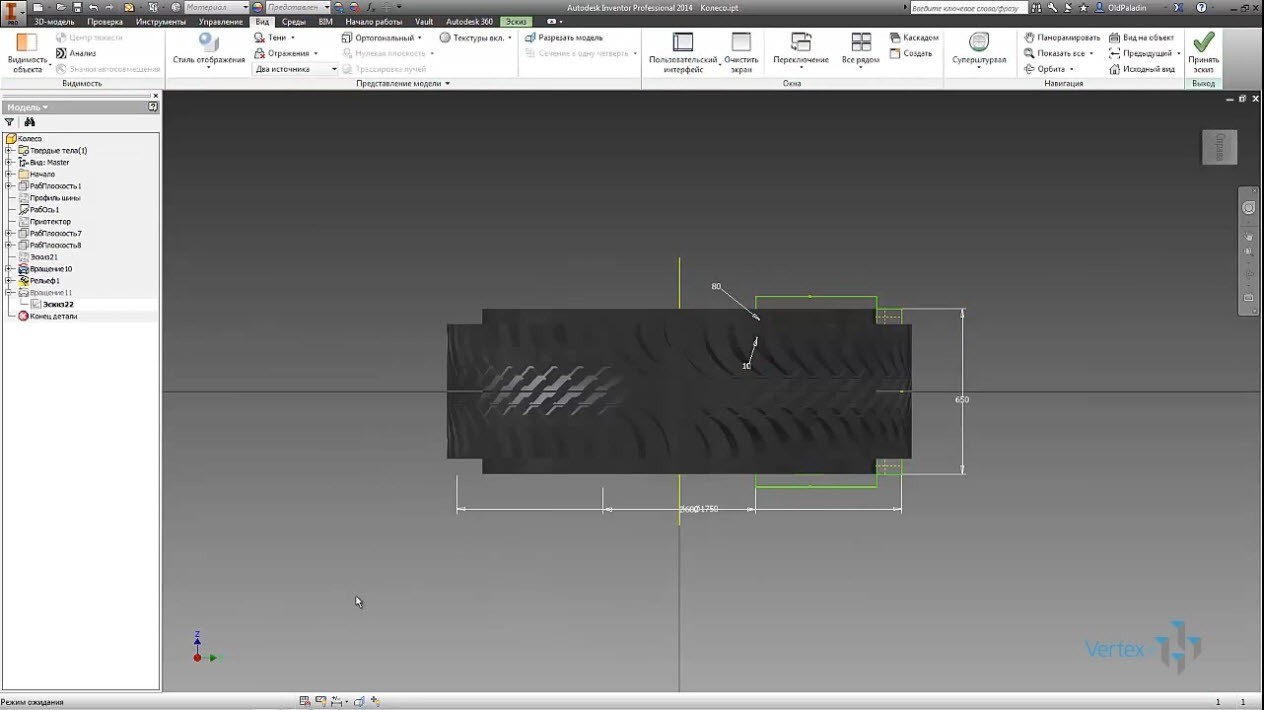
Убеждаемся еще раз приятной округлости боковых поверхностей, теперь нам нужно к цилиндрической поверхности на которой лежит рельеф протектора, добавить кривую поверхность, определяющую весь внешний образ покрышки.

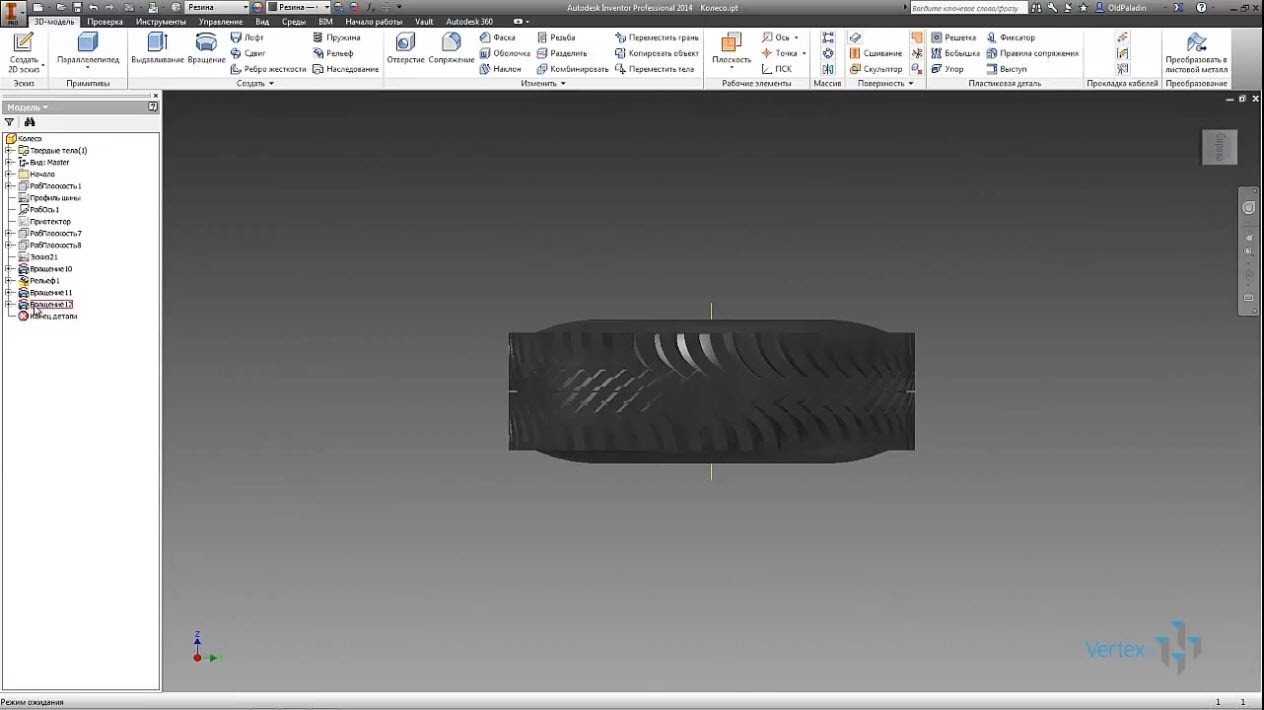
Для этого копируем эскиз профиля шины, работаем с ним, убираем с него все не нужное и добавляя замкнутый контур сообразующей кривой поверхности. Результат вот эта замкнутая область эскиза, которая будет нам нужна в качестве обрезающей поверхности.

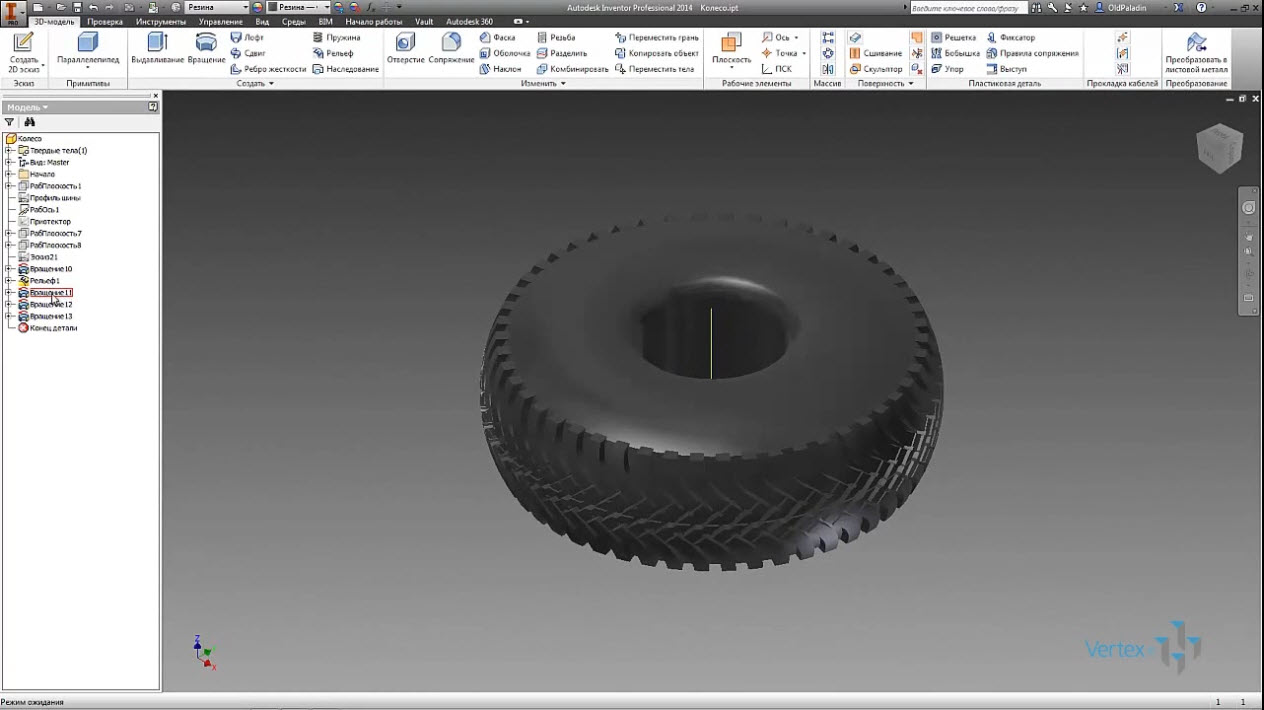
Видим резец с помощью которого сформируем кривую образующую поверхность. Проведя операцию вращения вокруг оси покрышки с вычитанием получаем посредством этого эскиза уже внешнюю кривую поверхность покрышки. Скопируем еще раз эскиз профиль и оставим только внутренний профиль.

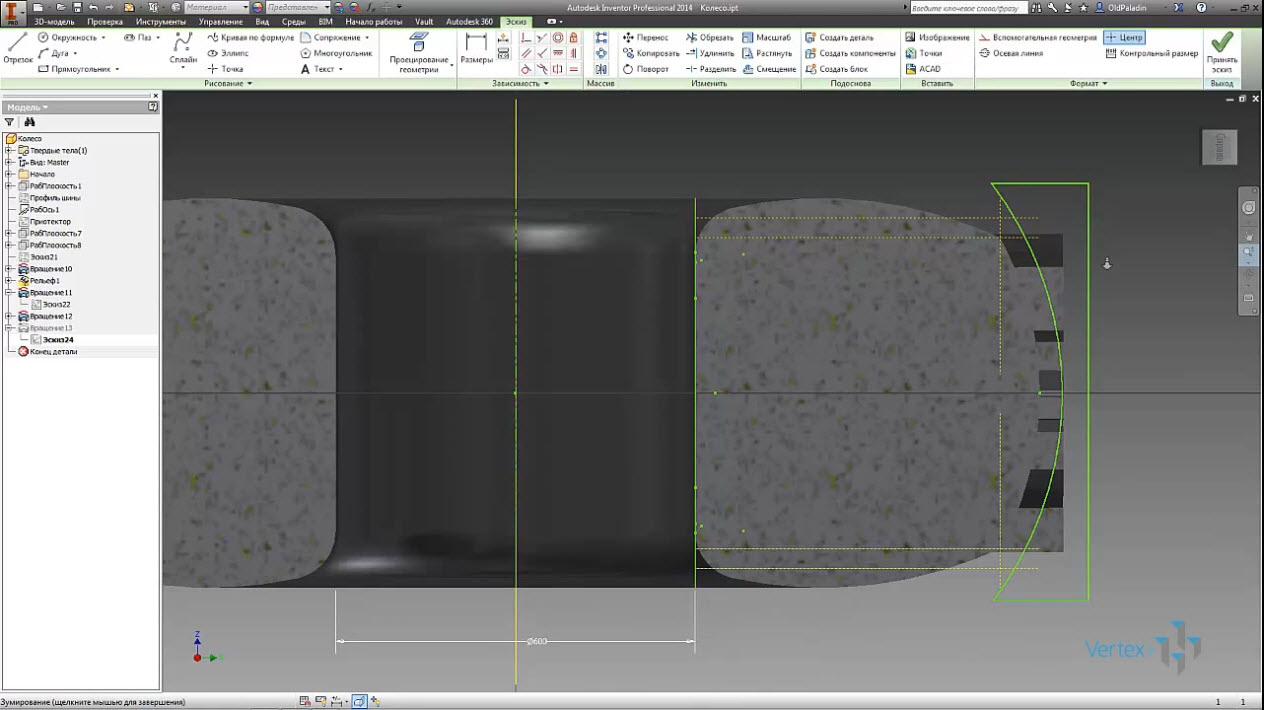
Вырезать внутреннюю часть шины, в которой размещается камера. На поперечном разрезе не хватает корда и слоев ткани, резины, такая детализация нам не нужна.

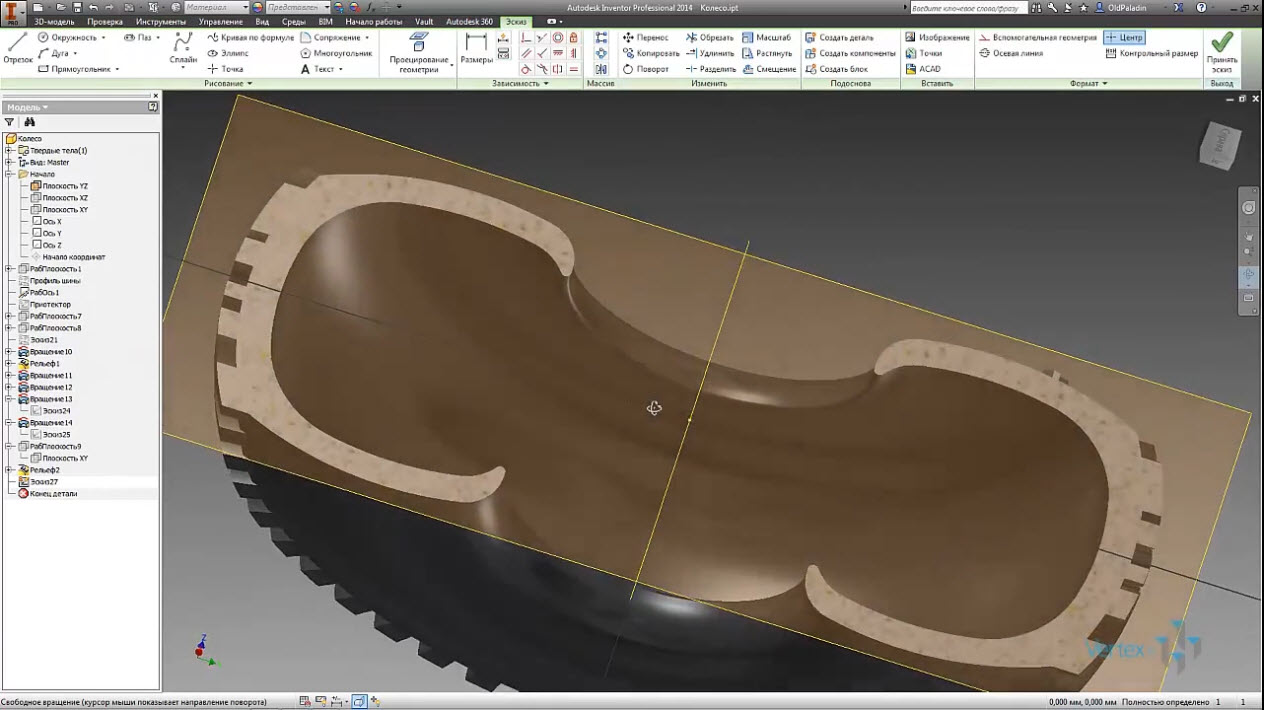
Если бы мы делали пресс-форму, то для каждой грани отдельных частей протектора пришлось бы выполнять операции снятие Фаски и сопряжение. Мы не делаем пресс-форму, результат нас устраивает.