В предыдущих главах были рассмотрены приемы построения чертежей в плоскости XY. Положение любой точки в этой системе координат характеризуются двумя значениями – абсциссой и ординатой. Для выполнения построений в трехмерном пространстве к этим координатам добавляется третья величина, определяющая объем того или иного изделия. Речь идет о координате Z, придающей плоским объектам объем. Умение правильно задавать координаты трехмерных объектов способствует корректному моделированию пространственных деталей. Для этих целей AutoCAD располагает тремя типами систем отсчета: трехмерные декартовые, цилиндрические и сферические координаты.
ДЕКАРТОВЫЕ КООРДИНАТЫ
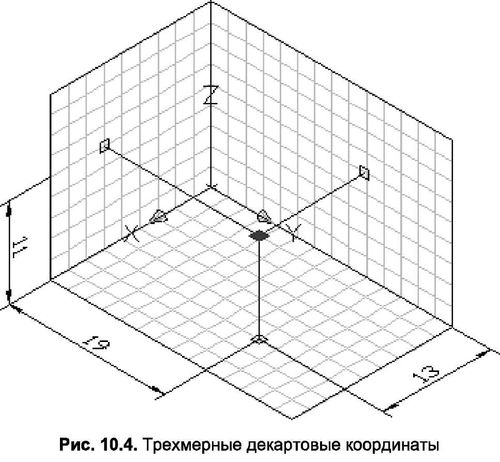
Для обозначения положения точки в трехмерном пространстве при помощи декартовых координат необходимо к значениям ее координат на плоскости XY добавить третье значение – координату Z. Так, например, на рис. 10.4 изображена точка, у которой координаты в плоскости XY равны 13.19, а по оси Z – 11 единиц.
При вводе координат в этой системе в первую очередь задается координата X, затем через запятую Y и только потом Z. Например: 13,19,11. Если числовое значение координаты дробное, то разделять целую и дробную части необходимо точкой. Кроме того, пробелы между числами и запятыми не допускаются.
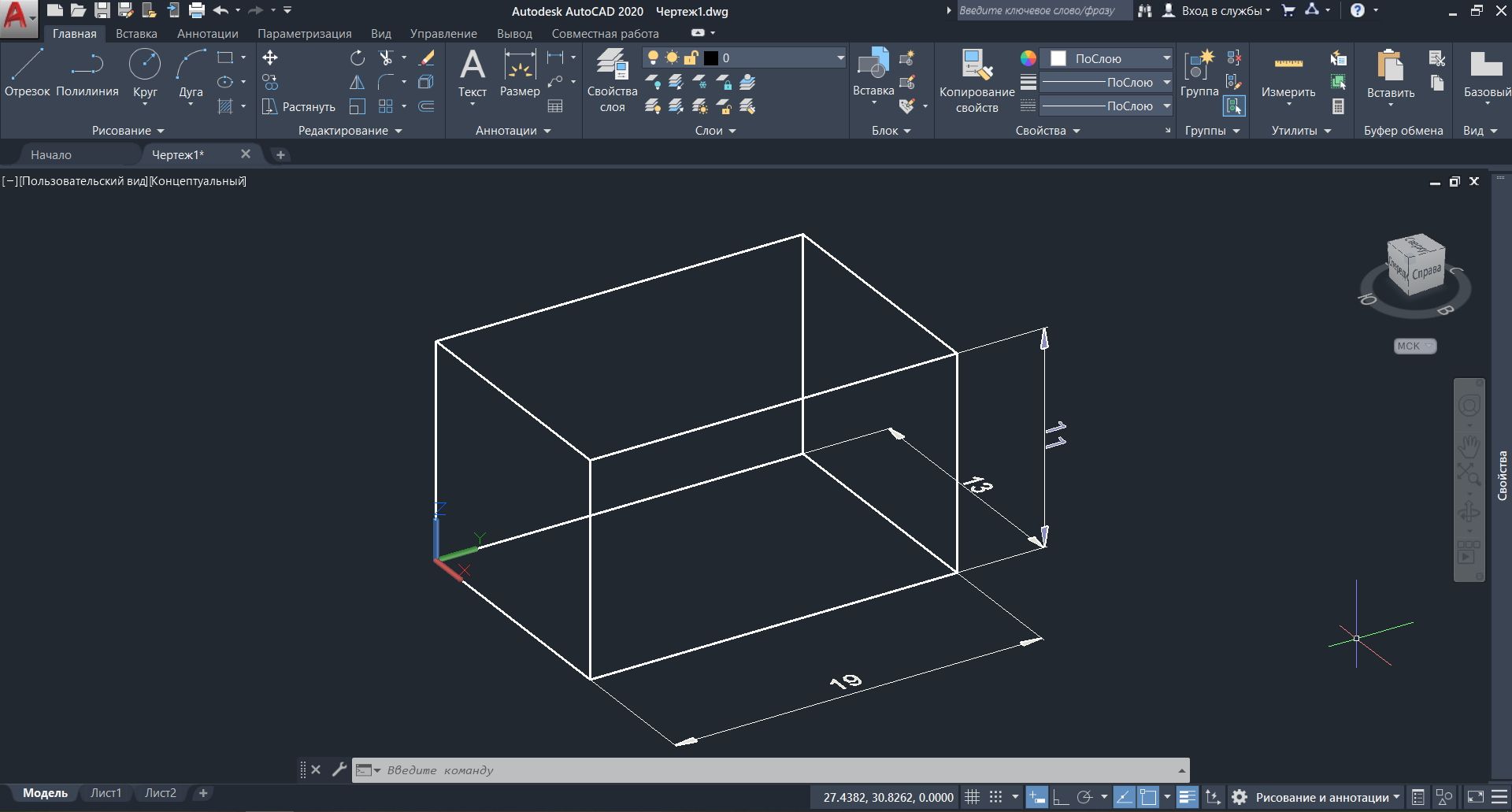
Попробуем построить параллелепипед из линий, с размерами 13,19,11, используя трехмерную систему координат. Для этого выберем Отрезок в главном меню. Для установки начальной точки параллелепипеда в координатах (0,0,0), воспользуемся динамическим вводом. После выбора Отрезка введем 0,0 Enter. Вместо «,» в динамическом вводе можно использовать клавишу TAB. В AutoCAD используются абсолютные и относительные координаты. В случае абсолютных координат, отсчет осуществляется от начала координат, а отсчет относительных координат осуществляется от последней поставленной точки и обозначается знаком @, абсолютных – знаком # перед вводом координат. Попробуем начертить параллелепипед, используя ввод координат.
У нас получился незаконченный параллелепипед, для завершения построения можно вручную дочертить 3 недостающие линии.
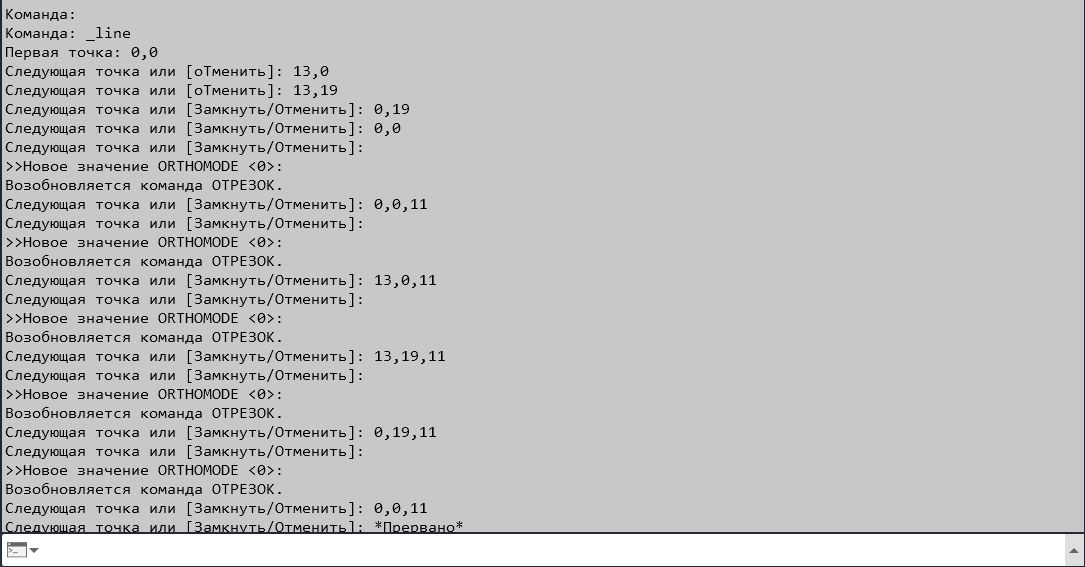
Пример ввода абсолютных координат для построения параллелепипеда.
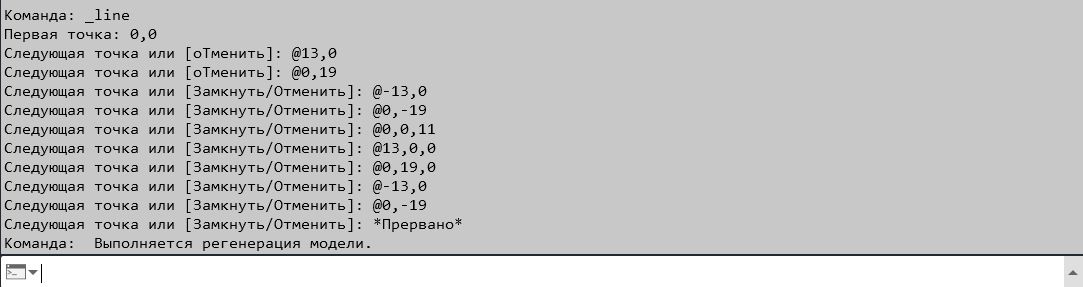
Пример ввода относительных координат для построения параллелепипеда.
После добавления недостающих линий и размеров. Как видим, получилось так, как и требовалось.
Примечание. Если при вводе координат в трехмерном пространстве пропущено значение Z, AutoCAD автоматически присвоит ему значение по умолчанию, записанное в системной переменной ELEVATION и называемое возвышением.
При создании трехмерных объектов используются понятия возвышения (уровня плоскости XY) и высоты. Возвышение определяется Z-координатой плоскости XY, на которой объект построен. Понятно, что если возвышение равно нулю (значение по умолчанию), то уровень объекта (его плоскость) совпадает с плоскостью XY. При положительном возвышении объект находится выше плоскости XY, а при отрицательном – ниже. Что касается высоты трехмерных объектов, то она определяет расстояние, на которое объект смещен относительно возвышения.
Обычно к редактированию параметров возвышения и высоты прибегают в случае, когда необходимо построить несколько точек, у которых координата Z имеет одно и то же значение. Упрощение построений вызвано тем, что при этом достаточно будет вводить для каждой такой точки только два значения, определяющих ее положение в плоскости XY.
Как уже было отмечено, текущее значение возвышения хранится под именем системной переменной ELEVATION, а высоты – переменной THICKNEES. Для того чтобы изменить значение обоих параметров, присваиваемое вновь созданным объектам, нужно выполнить команду Elev и ответить на следующие вопросы:
Command: Elev
Specify new default elevation <0.0000>: <Ввод нового значения возвышения>
Specify new default thickness <0.0000>: <Ввод нового значения высоты>
Также следует отметить, что значение высоты объекта можно менять из палитры Свойства (Properties).
ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ
Положение точки в цилиндрических координатах также определяется тремя величинами, однако одно из них – угловое.
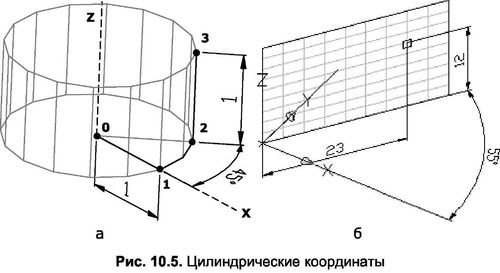
Как известно, круговой цилиндр образуется путем вращения образующей 2-3 (рис. 10.5а) по окружности, описывая угол 360°. Именно этот принцип положен в концепцию цилиндрических координат. Определяя положение точки, необходимо задать вначале радиус цилиндра (0-1), затем угол вращения образующей (1-2) и, наконец, высоту цилиндра (2-3). Так, например, точка, изображенная на рис. 10.36, была построена относительно текущей ПСК после ввода в командную строку 23<55,12. Значок «<» указывает на то, что после него вводится числовое значение угла поворота образующей, запятая перед этим значком не ставится, а после величины угла – должна вводиться обязательно. Таким образом, в цилиндрической системе координат положение точки определяется в следующем порядке: радиус – угол – образующая.
Следует обратить внимание на правило знаков. Что касается линейных координат, то тут все просто – направление осей определяет положительные значения отсчета. При этом положительное направление оси Z можно контролировать правилом правой руки. Это правило заключается в следующем. Если большой палец правой руки совместить с осью X, а указательный – с осью Y, то остальные пальцы в изогнутом положении укажут положительное направление оси Z (рис. 10.56).
Для определения положительного направления вращения относительно любой оси нужно следовать следующему правилу. Если установить наблюдателя со стороны положительного направления оси, то положительное направление отсчета углов будет совпадать с движением против часовой стрелки (рис. 10.4). Таким образом, чтобы ввести направление угла по часовой стрелке, значение угла следует вводить со знаком минус.
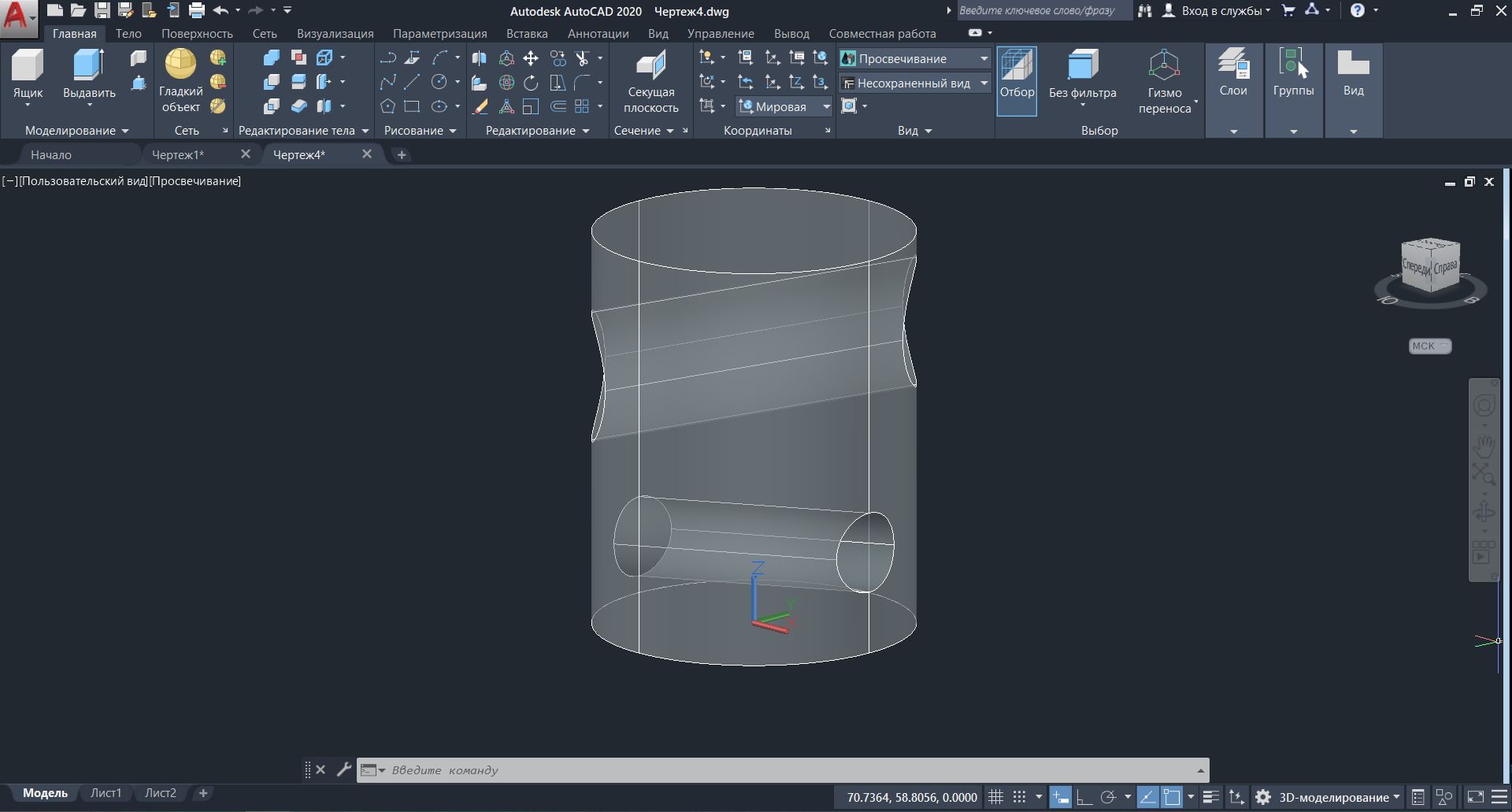
Для примера построим цилиндр с несколькими отверстиями, расположенными под разными углами. Для начала создадим оси будущих отверстий, с помощью ввода координат. Ниже приведен пример ввода абсолютных и относительных цилиндрических координат.
Для создания осей отверстий используем такие координаты:
0,0,10
25<0,8
0,0,35
25<45,10
Пропустим последующие построения с использованием ПСК и вычитания твердых тел, так как они будут рассматриваются в других уроках и посмотрим результат, который получился в итоге.
СФЕРИЧЕСКИЕ КООРДИНАТЫ
Положение точки в сферических координатах определяется также тремя величинами, из которых одно линейное, а два остальных – угловые.
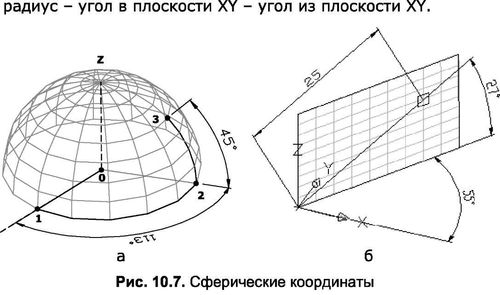
Как известно, сферическая поверхность представляет собой геометрическое место точек пространства, равноудаленных от одной точки – центра шара. Поэтому, чтобы определить положение точки, расположенной на поверхности сферы (рис. 10.7а), достаточно указать радиус окружности, вращением которой образуется шар (0-1), затем угол, образованный вращением окружности вокруг оси Z (1-2), и наконец, угол, образованный вращением окружности относительно оси X (2—3). Так, например, точка, изображенная на рис. 10.76, была построена относительно текущей ПСК после ввода в командную строку 25<55<27. Значок «<» указывает на то, что после него вводится числовое значение угла поворота образующей. Таким образом, в сферической системе координат положение точки определяется в следующем порядке:3
Сферические координаты, так же как и предыдущем примере, могут использоваться для дополнительных построений на выпуклых и вогнутых поверхностях.
ФИЛЬТРЫ ТОЧЕК
Координатные фильтры точек – это еще один способ ввода координат в трехмерном пространстве, отличительной чертой которого является зависимость от координат ранее введенных объектов. Другими словами, чтобы назначить координаты этим способом, нужно привязаться к узлам уже существующих объектов для автоматического извлечения из них заказанной вами координаты.
Примечание. Задание координат в трехмерном пространстве способом фильтрации точек может быть эффективно только при использовании режимов объектной привязки.