Метод сфер | AutoCAD

Еще один метод построения линии пересечения поверхностей вращения – метод сфер. Он применяется в случаях, когда метод секущих плоскостей использовать нецелесообразно – например, когда оси одной или обеих поверхностей вращения расположены так, что при пересечении этих поверхностей с плоскостями, параллельными плоскостям проекций, образуются сложные фигуры. Один из таких случаев – когда оси поверхностей вращения пересекаются в пространстве. Пусть одна из поверхностей – цилиндр, а вторая – тело вращения, образованное кривой 2-го порядка. Оговоримся, что для применения метода сфер необходимо привести чертеж к такому виду, когда оси вращения обеих поверхностей параллельны одной из плоскостей проекций.

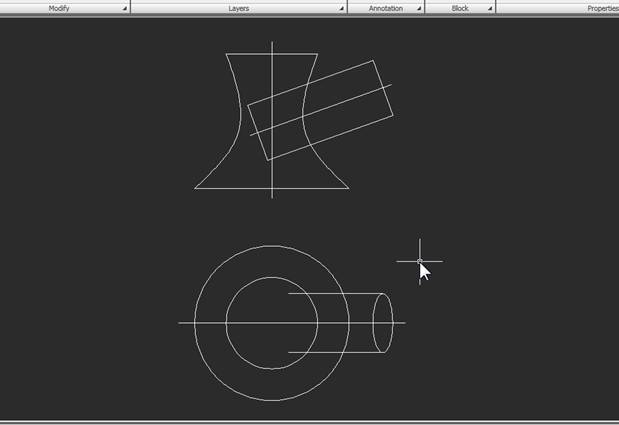
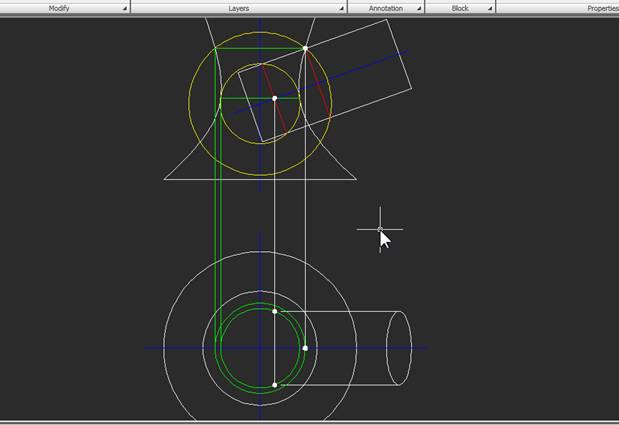
1. Пусть исходный чертеж выглядит так:

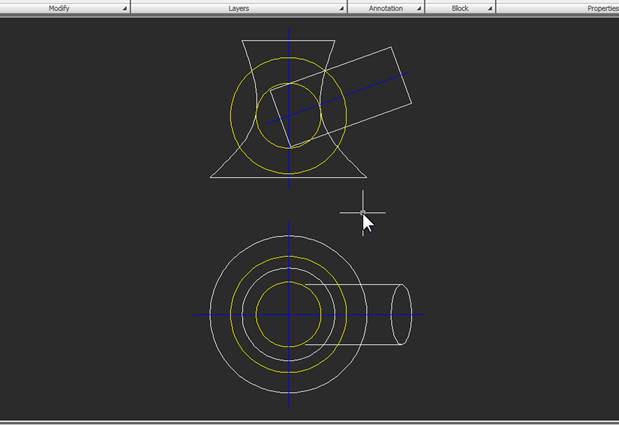
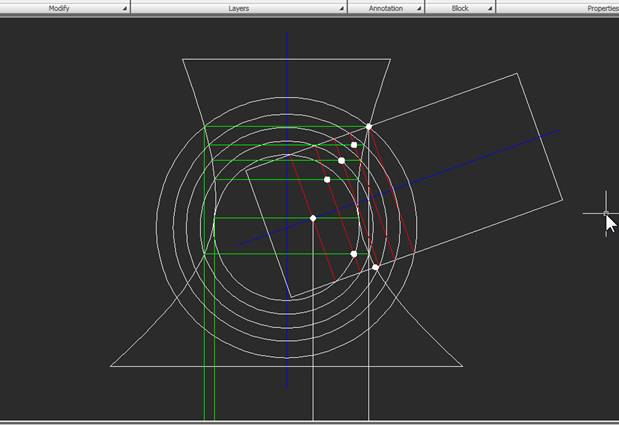
2. При построениях такого рода целесообразно применять концентрические сферы-посредники, центры которых расположены в точке пересечения осей исходных тел вращения. Эти сферы, пересекаясь с исходными телами, образуют окружности, а искомые точки линии пересечения будут общими точками пар окружностей, принадлежащим двум телам.  Построим «крайние» сферы – самую большую и самую малую из всего диапазона. Видно, что самая большая из сфер пройдет через наиболее удаленную от центра точку пересечения поверхностей, а самая малая будет касаться «внутренней» поверхности одного из тел (сферы меньшего диаметра уже не пересекают оба тела, т.е. в построении не участвуют).

 Эти сферы дадут нам первые точки пересечения поверхностей. Находим их так: сначала строим линии пересечения сферы-посредника с каждым из тел на фронтальном виде. Эти линии – окружности, которые на фронтальном виде превращаются в прямые:

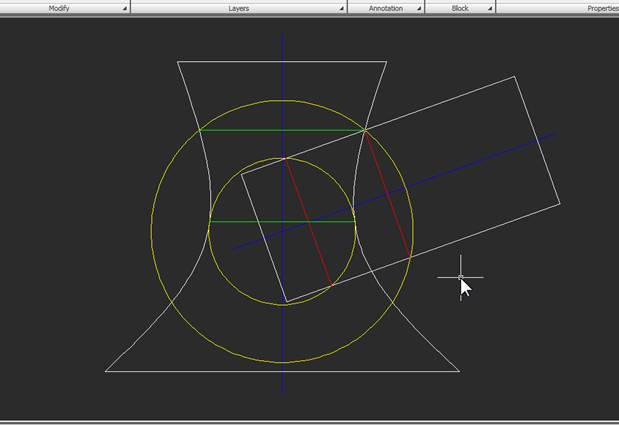
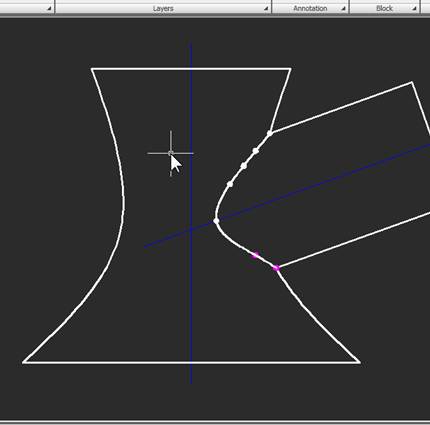
 3. Пересечение двух линий, образованных одной сферой, даст соответствующую точку искомой линии пересечения поверхностей (поскольку линия симметрична относительно вертикальной плоскости, в которой лежат оси обоих тел, на фронтальном виде будем строить только видимую часть линии. Итак, вот две первые точки:

 Переносим эти точки на вид сверху. Здесь важно понимать следующее: точки лежат на окружностях, образованных пересечением сфер-посредников с каждым из тел, причем это утверждение справедливо для любых проекций. Поэтому нам нужно построить эти окружности на виде сверху для любого из тел (очевидно, что цилиндр в этом случае неудобен, поскольку его ось наклонена) и перенести на них точки с фронтального вида. Сферы, изображенные на виде сверху, можно удалить, чтобы они не мешали построениям:

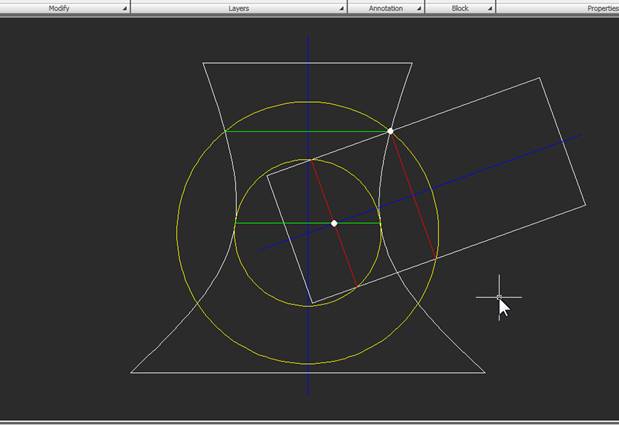
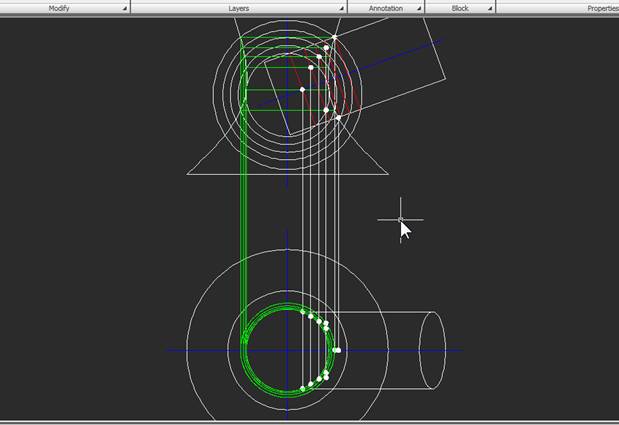
 4. Построим еще несколько сфер-посредников, охватывающих всю область пересечения тел. Одна из сфер должна пройти через вторую «пиковую» точку – самую нижнюю точку пересечения поверхностей. Кстати, строить эту сферу необязательно – эта точка, как и верхняя, явно видна на чертеже. Вот результаты построений для фронтальной проекции:

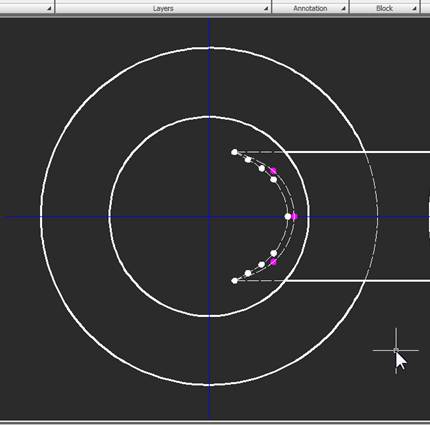
 И для вида сверху:

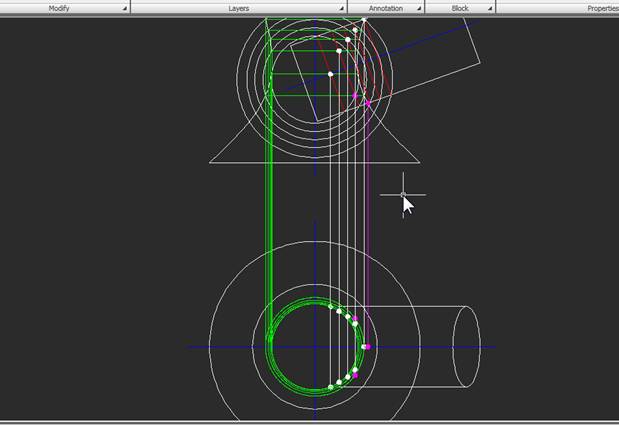
 Для того, чтобы не запутаться в множестве линий построения, можно удалять их после нахождения каждой точки. Также полезно выделить точки, находящиеся на виде сверху ниже «границы видимости», другим цветом. Эти точки на фронтальном виде расположены ниже оси цилиндра. Точка, отделяющая «нижние» точки от «верхних», лежит на оси цилиндра. В нашем случае она практически совпадает с точкой, лежащей на малой сфере, вообще же она требует отдельного построения:

[ads]

 После соединения полученных точек командой Spline и удаления всех вспомогательных линий получим такие результаты:

 Стоит отметить, что команда Spline может не сразу дать правильное отображение линии пересечения, особенно на виде сверху. Может оказаться целесообразным рисовать отдельно «правую» и «левую» части кривой.

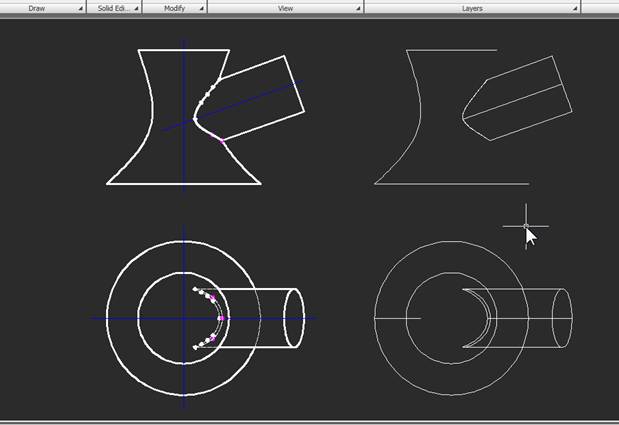
5. Осталось только сравнить наши построения с пересечением двух поверхностей, которое Autocad строит автоматически. Для этого изобразим исходные тела с помощью команд 3D-моделирования, объединим их и расположим рядом с полученными чертежами:

 Как видим, метод сфер позволяет достаточно адекватно изображать пересечение сложных поверхностей вращения. И хотя сегодня он носит достаточно иллюстративный характер, разобраться в нем очень полезно для понимания основ геометрии и трехмерного моделирования.