Вспомогательные объекты

В этом простом уроке покажем, как в Autocad можно использовать вспомогательные трехмерные объекты, если для какой-либо задачи не хватает стандартных средств (привязок, трассировок и т.д.)

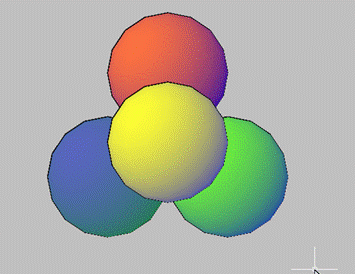
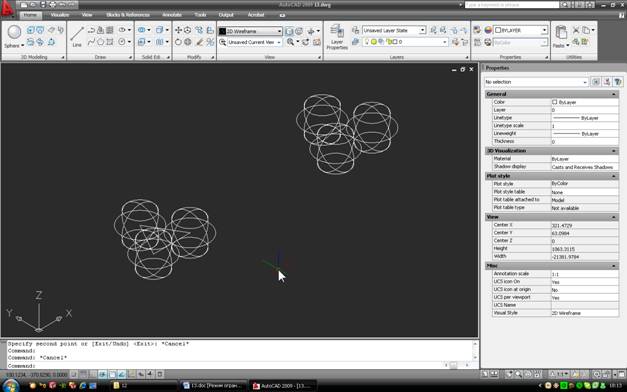
Пусть нужно построить «пирамидку» из четырех одинаковых шаров, которые касаются друг друга. Задача довольно абстрактна, но приемы, которые мы в ней рассмотрим, довольно полезны. Для начала покажем, что мы хотим построить (в изометрии и на виде сверху):

 Каждый шар должен касаться трех остальных – таково условие задачи. Итак, начнем. Работать, естественно, будем в интерфейсе 3D Modelling.

1. Попробуем разобраться в сути задачи. Нарисовать сферу – дело простое. Две смежные – тоже: достаточно скопировать первую на расстояние 2R, где R – радиус сферы. Но как быть с третьей и четвертой? Вопрос о трех сферах решается тоже довольно просто – их центры лежат в вершинах равностороннего треугольника, сторона которого равна тем же 2R. А вот для четвертой понадобится дополнительное построение.

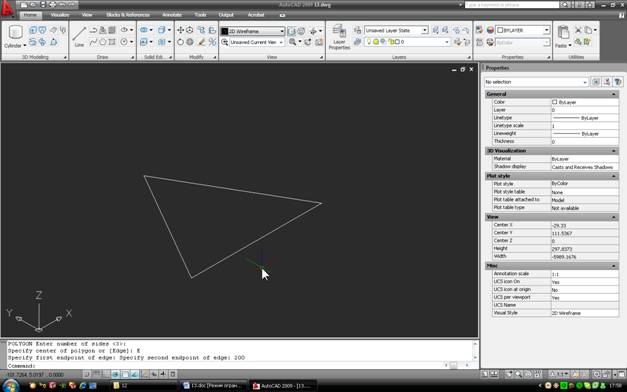
Пусть радиус сферы равен 100мм. Создадим первые три сферы. Для этого построим равносторонний треугольник со стороной 2*100=200мм. Строится он командой Polygon панели Draw.

 Взяв команду и сразу введя количество сторон (3), нужно затем по правому клику перейти в экранное меню и выбрать опцию Edge – построение многоугольника по длине стороны. После этого показываем первую точку и, задав направление, вводим длину стороны (200) и жмем Enter. Получим такой треугольник:

 2. Разместим в его вершинах сферы с радиусом 100мм. Сфера рисуется просто, радиус задаем с клавиатуры. Затем копируем первую сферу, которую мы рисовали непосредственно из вершины треугольника, за центр в две другие вершины. Должен получиться такой результат:

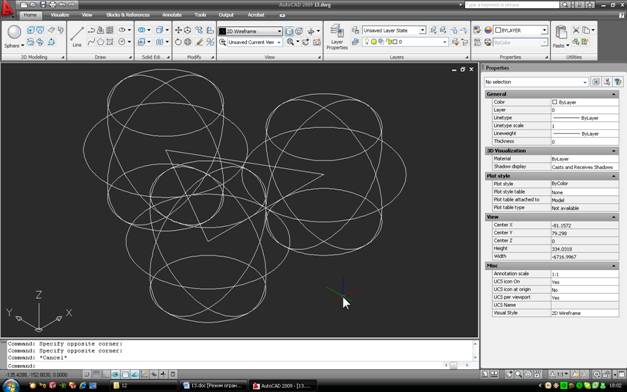
 3. Пока сдвинем три сферы в сторону по одной из осей координат, скажем, на 1000мм, и попытаемся понять, что же делать дальше. Ясно, что задача похожая, но теперь центр последней сферы должен отстоять на 200мм от каждой из трех вершин исходного треугольника (тогда эта новая сфера будет касаться каждой из уже существующих). Из школьного курса геометрии можно, поднатужившись, вспомнить, какая фигура в пространстве ограничивается точками, отстоящими от исходной на одно и то же расстояние. Эта фигура – опять же, сфера. То есть, чтобы найти точки, отстоящие от двух вершин на одно и то же расстояние, нужно построить из этих вершин две одинаковые сферы, линия пересечения которых и будет искомым множеством точек. Аналогично, если построить сферы с центрами в трех точках, то у всех трех сфер будет всего две общие точки, которые и будут удовлетворять условию. На практике нам просто нужно построить три сферы с радиусом 200мм (межцентровое расстояние двух 100-миллиметровых сфер) в трех вершинах треугольника, а затем найти их пересечение.

[ads]

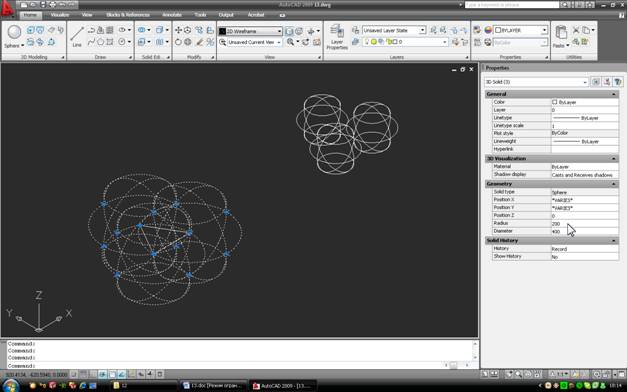
4. Проще всего скопировать обратно наши исходные сферы и увеличить их радиус:

 Выделим три сферы, расположенные на треугольнике. В окне свойств изменим радиус всех трех со 100мм на 200мм:

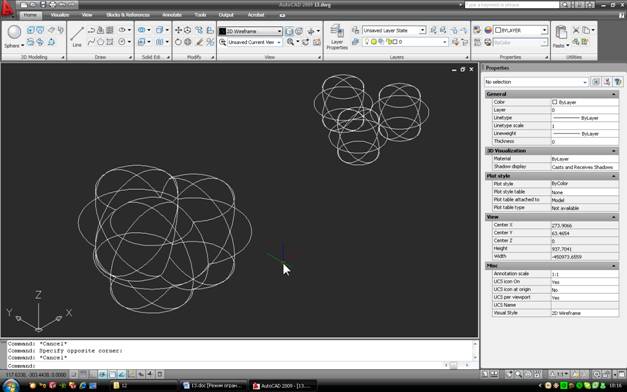
 Теперь удалим треугольник и объединим три большие сферы в один объект командой Union (панель Solids Editing):

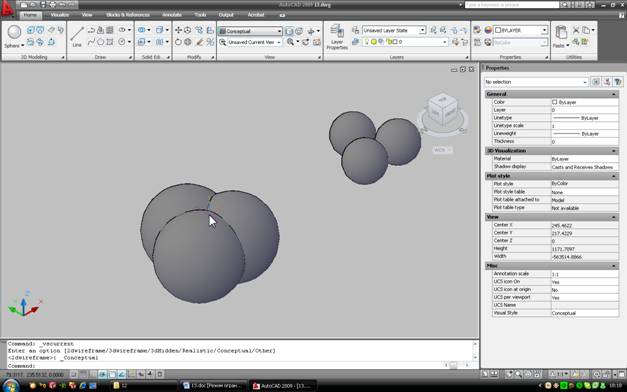
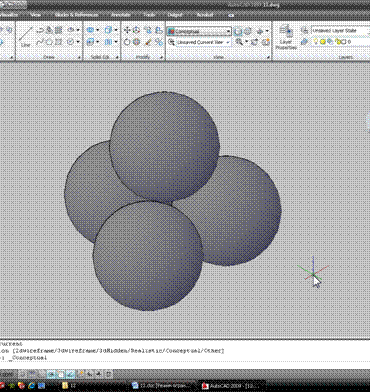
 В кажущемся хаосе линий можно, постаравшись, разглядеть точку, где сходятся стыки сфер. Вообще-то таких точек две, но нас интересует только верхняя. Если вы все-таки не можете понять, о какой точке идет речь – можно включить отображение Conceptual, и увидеть такую картину:

Курсор на этой картинке находится рядом с нужной нам точкой.

5. Осталось скопировать любую из маленьких сфер центром в эту точку, используя привязку Endpoint, а затем удалить вспомогательные большие сферы и вернуть три маленькие на свое место, сдвинув их на 1000мм:

 Задача решена. Все четыре сферы именно касаются друг друга – это легко проверить, попытавшись «впечатать» одну сферу в другую командой Imprint (Solids Editing) – после выполнения этой команды на первой сфере из выбранной пары останется характерная точка – отпечаток второй сферы.

Метод, который мы применили в этой выдуманной задаче, будет полезным в реальном моделировании – часто гораздо проще нарисовать один или несколько вспомогательных объектов, чтобы с их помощью выполнить необходимое построение, причем Autocad, в отличие от кульмана, позволяет делать все это в трехмерном пространстве.

На этом данный урок закончен! Ждем Ваших оценок и комментариев ниже!