На цьому нехитрому уроці ми покажемо, як автокад може використовувати допоміжні тривимірні об’єкти, якщо в завданні відсутні стандартні інструменти (палітурки, сліди і т.д.)
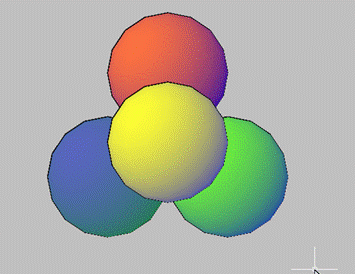
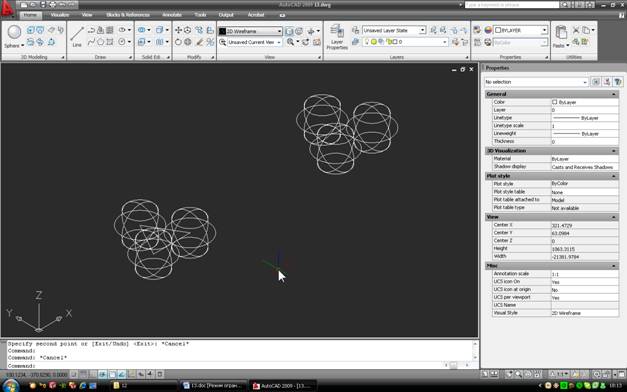
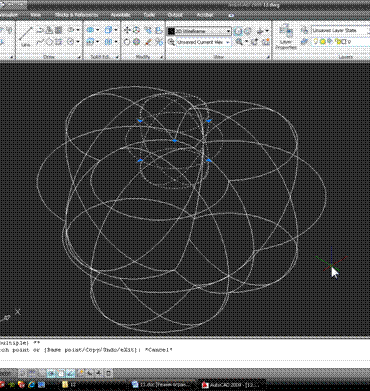
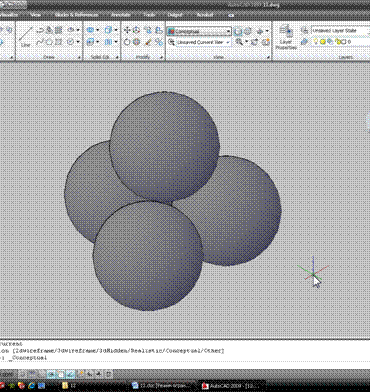
Побудуємо «піраміду» з чотирьох однакових кульок, які торкаються один одного. Завдання досить абстрактна, але прийоми, які ми в ній розглянемо, досить корисні. Для початку покажемо, що ми хочемо побудувати (в ізометрії і на верхньому виді):
Кожен м’яч повинен торкнутися трьох інших – в цьому і полягає умова проблеми. Отже, приступимо. Природно, ми будемо працювати в інтерфейсі 3D-моделювання.
1. Спробуємо зрозуміти суть завдання. Малювання сфери – справа нескладна. Два суміжних – теж: досить скопіювати перший на відстані 2R, де R – радіус сфери. А як щодо третього і четвертого? Питання про трьох сферах також вирішується досить просто – їх центри лежать в вершинах рівностороннього трикутника, сторона якого дорівнює тим же 2R. А ось для четвертого знадобиться додаткова збірка.
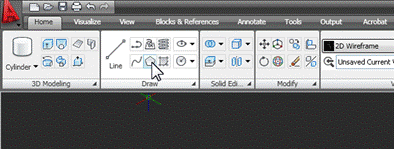
Нехай радіус сфери буде 100мм. Створимо перші три сфери. Для цього спорудити рівносторонній трикутник зі стороною 2 * 100 = 200мм. Він побудований командою Polygon панелі Draw.
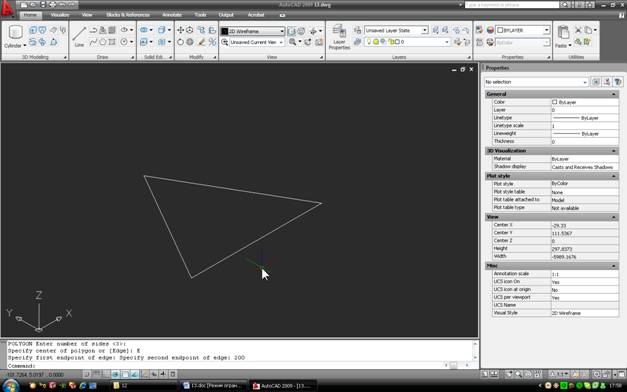
Взявши команду і відразу ввівши кількість сторін (3), потрібно потім натиснути правою кнопкою миші, щоб перейти в екранне меню і вибрати опцію Edge – побудова багатокутника по довжині збоку. Після цього покажіть першу точку і, задавши напрямок, введіть довжину сторони (200) і натисніть Enter. Давайте отримаємо такий трикутник:
2. Помістіть в її вершини сфери радіусом 100 мм. Сфера малюється просто, радіус задається від клавіатури. Потім копіюємо першу сферу, яку намалювали прямо з вершини трикутника, за центром в дві інші вершини. Результат повинен бути наступним:
3. Поки що відсуньте три сфери в сторону по одній з осей координат, скажімо, на 1000 мм, і спробуйте зрозуміти, що робити далі. Зрозуміло, що проблема аналогічна, але тепер центр останньої сфери повинен бути в 200мм від кожної з трьох вершин вихідного трикутника (тоді ця нова сфера торкнеться кожної з існуючих). Зі шкільного курсу геометрії можна, напружуючись, згадати, яка фігура в просторі обмежена точками, відокремленими від оригіналу на однакову відстань. Ця цифра є, знову ж таки, сферою. Тобто для того, щоб знайти точки, відокремлені від двох вершин однаковою відстанню, необхідно побудувати з цих вершин дві однакові сфери, лінія перетину яких буде потрібною множиною точок. Аналогічно, якщо будувати сфери з центрами в трьох точках, то у всіх трьох сфер буде всього два загальних моменти, які задовольнять умову. На практиці нам просто потрібно побудувати три сфери радіусом 200мм (центральна відстань двох 100мм сфер) в трьох вершинах трикутника, а потім знайти їх перетин.
[ads]
4. Найпростіший спосіб – скопіювати назад наші оригінальні сфери і збільшити їх радіус:
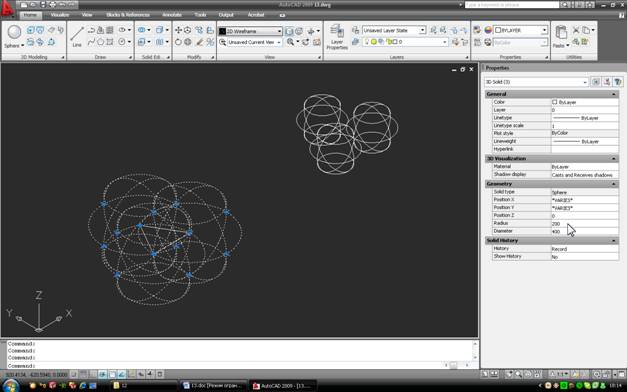
Виділимо три сфери, розташовані на трикутнику. У вікні властивостей змініть радіус усіх трьох з 100 мм на 200 мм:
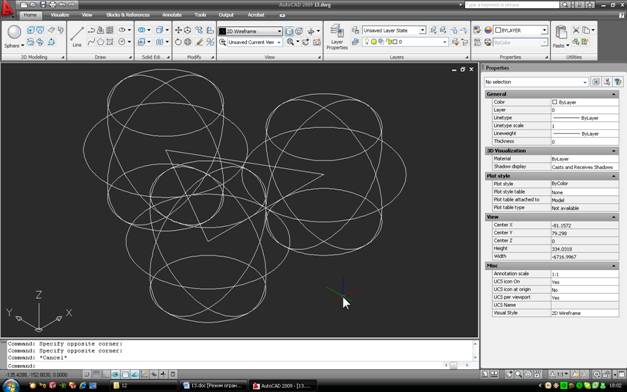
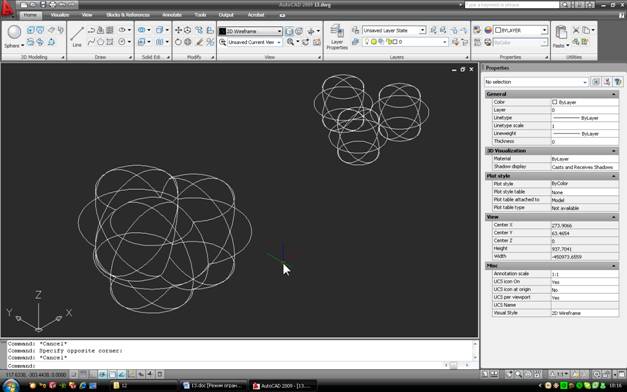
Тепер давайте приберемо трикутник і об’єднаємо три великі сфери в один об’єкт командою “Об’єднання ” (панель “Редагування твердих тіл”):
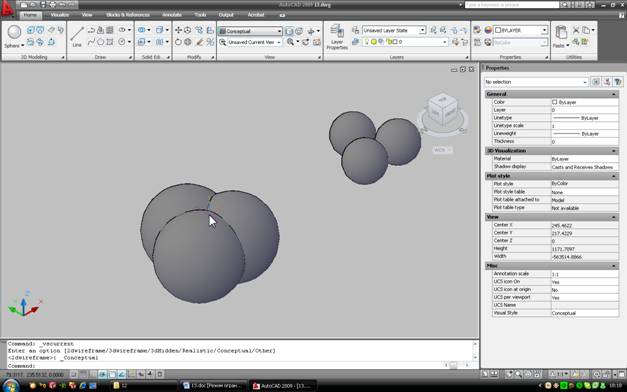
У видимому хаосі ліній можна, намагаючись розгледіти точку, де сходяться суглоби сфер. Власне, таких моментів два, але нас цікавить тільки верхній. Якщо ви все ще не можете зрозуміти, про який момент йдеться – можна включити Концептуальний дисплей, і подивитися цю картину:
Курсор на цій картинці знаходиться поруч з потрібною нам точкою.
5. Все, що залишилося, – це скопіювати будь-яку з малих сфер, зосереджених до цієї точки, за допомогою прив’язки Endpoint, а потім видалити допоміжні великі сфери і повернути три малі на своє місце, перемістивши їх на 1000 мм:
Проблема вирішена. Всі чотири сфери торкаються один одного – це легко перевірити, спробувавши «відбиток» однієї сфери в іншу командою Imprint (Solids Editing) – після виконання цієї команди на першій сфері обраної пари залишиться характерна точка – відбиток другої сфери.
Метод, який ми використовували в цій вигаданій задачі, буде корисний при реальному моделюванні – часто набагато простіше намалювати один або кілька допоміжних об’єктів, щоб використовувати їх для виконання необхідної конструкції, а Autocad, на відміну від кульмана, дозволяє все це робити в тривимірному просторі.
На цьому цей урок закінчується! Чекаємо ваших оцінок і коментарів нижче!