Еліпсів

КОМАНДА «ЕЛІПС»

Еліпс характеризується координатами центру, а також розмірами його великої і малої осей.

Побудова еліпсів в AutoCAD здійснюється командою Ellipse, яку, крім прямого входу клавіатури, можна викликати за допомогою кнопки Еліпс, розташований у групі інструментів “Креслення” на вкладці “Примітка”(Основне)...

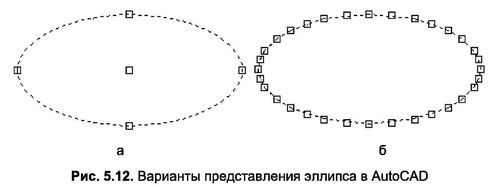
За замовчуванням AutoCAD будує еліпс у вигляді одного об’єкта, що визначається координатами геометричного центру і кінцевими точками осей (рис. 5.12а). При переміщенні опорних точок в цьому випадку змінюються як розміри осей, так і розміри самого еліпса. Іноді таке уявлення фігури може бути незручним, і в таких ситуаціях можна використовувати наближений варіант еліпса.

Для того щоб наблизити поверхню еліпса дугами кіл, необхідно встановити системну змінну PELLIPSE на 1 (за замовчуванням встановлено значення 0). В цьому випадку при виділенні еліпса відображаються граничні точки всіх дуг (рис. 5.126). Однак при такому способі представлення еліпса його геометричний центр і граничні точки головних осей не будуть показані.

За замовчуванням еліпс будується в початковій і кінцевій точках першої осі і точці на одному кінці другої осі. При цьому координати точок можуть бути введені з командного рядка або вказані мишкою. Цей метод побудови можна змінити, вибравши один з наступних варіантів уточнення:

Вкажіть кінцеву точку осі еліпса або [Arc/Center]: <Введіть координати першої точки, яка визначає положення однієї з осей еліпса, або виберіть один з параметрів>
Вкажіть іншу кінцеву точку осі: <Введіть координати другої точки осі еліпса>
Вкажіть відстань до іншої осі або [Rotation]: зпозицією другої осі>

Параметри команд наступні:

• Дуга – використовується для побудови еліптичних дуг;
• Центр – дозволяє побудувати еліпс в точці геометричного центру дуги і точках, розташованих на кінцях її осей;
• Обертання – дозволяє намалювати еліпс у вигляді проекції на площину кола, діаметр якого є першою заданою віссю еліпса, яка автоматично приймається за велику.

ПОБУДОВА ЕЛІПСА ВЗДОВЖ ГРАНИЧНИХ ТОЧОК ПЕРШОЇ ОСІ І ТОЧКИ, РОЗТАШОВАНОЇ НА ОДНОМУ КІНЦІ ДРУГОЇ ОСІ (ОСІ, КІНЦЯ)

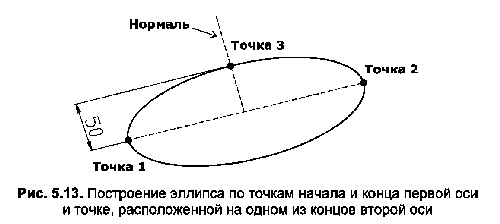
Як уже зазначалося, такий спосіб побудови еліпса пропонується автоматично. Для зазначеної осі кінцевої точки питання еліпса досить вказати координати першої точки першої осі, а для другого питання Вказати іншу кінцеву точку осі – координати другої точки (рис. 5.13).

На наступне питання (Вкажіть відстань до іншої осі або [Rotation]) можна відповісти по-різному, що визначає вибір одного з трьох можливих методів.

Якщо ввести відстань (в даному випадку 50), то прийнято дорівнювати половині довжини другої осі. При введенні координат точки відстань від неї до середини першої осі також вважається половиною довжини другої осі. Однак еліпс пройде через зазначену точку тільки в тому випадку, якщо він лежить на нормальній (перпендикулярної) до першої осі, що виходить від її середини. Якщо вказати параметр Обертання, то він буде означати перехід до принципово іншого методу – проекції на площину побудови уявного кола.

ПОБУДОВА ЕЛІПСА З ПРОЕКЦІЇ НА ПЛОЩИНІ ПОБУДОВИ УЯВНОГО КОЛА (ОБЕРТАННЯ)

Цей метод заснований на використанні проекції на площину екрану уявного кола діаметром, рівним довжині першої заданої осі. При цьому вісь, задана координатами точок 1 і 2, автоматично приймається за велику, а положення другої осі визначається кутом нахилу проектованого кола щодо площини побудови. Під кутом нахилу, рівним його мінімальному значенню (0°), еліпс перетворюється в коло, а максимальне значення кута (89,4°) робить еліпс фігурою, що наближається за зовнішнім виглядом до прямої лінії.

ПОБУДОВА ЕЛІПСА В ТОЧЦІ ЙОГО ЦЕНТРУ І ТОЧОК, РОЗТАШОВАНИХ НА КІНЦЯХ ОСЕЙ (ПО ЦЕНТРУ)

Цей параметр дозволяє побудувати еліпс (рис. 5.14) шляхом вказівки координат його геометричного центру (точки 4), а також точок, розташованих на одному кінці обох осей (точка 2, точка 3).

Єдина відмінність цього методу від Осі, Кінець полягає в тому, що для першого питання (Вкажіть вісь кінцевої точки еліпса або [Arc/Center]) замість того, щоб вказувати положення першої точки, необхідно ввести параметр C (Center), а потім для зазначення центру питання еліпса визначити положення геометричного центру фігури.

Можливе поєднання розглянутого методу з методом обертання (побудова еліпса з проекції на площину побудови уявного кола).