Давняя загадка
Обычно делюсь с читателями результатом, но сейчас делюсь загадкой, которую загадал мне мой Autodesk Inventor Professional 2021.
Много лет меня буквально преследовала, «доставала» мысль о динамической системе, похожей на сообщающиеся сосуды, но, чтобы вместо воды – кинетическая энергия и, в идеале, чтобы процесс был незатухающий.
Разумеется, идеал недостижим – всегда вмешивается трение. Но можно же и «подпитывать» энергией, как с классическим маятником Гюйгенса в «ходиках».
Однажды такая система нашлась. Конечно же, чисто «случайно» – работал над какой-то совсем другой конструкцией. Нахально считаю ее своею, поскольку ничего похожего не видел. Буду не очень рад, но переживу, если «товарищи меня поправят».
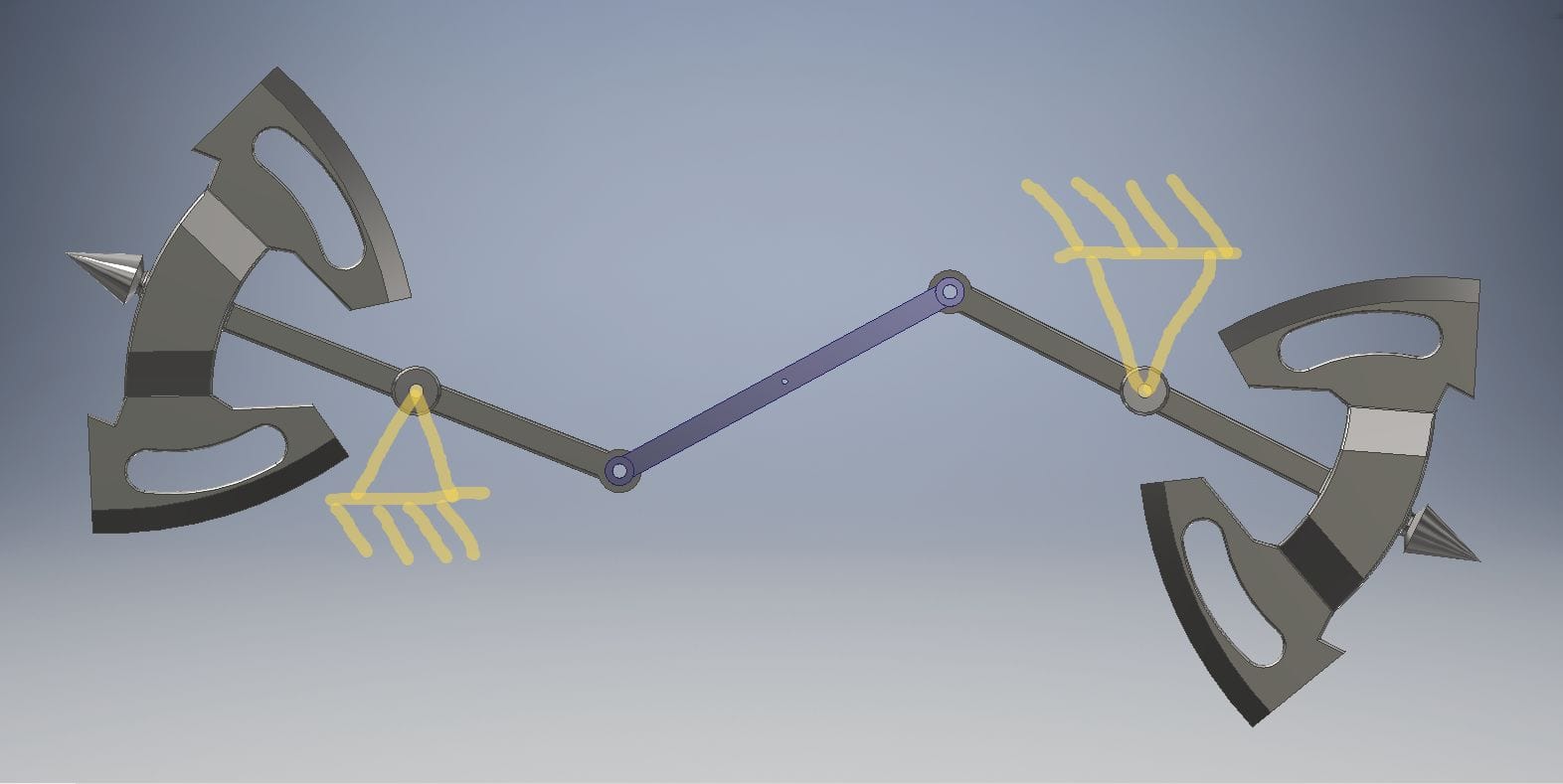
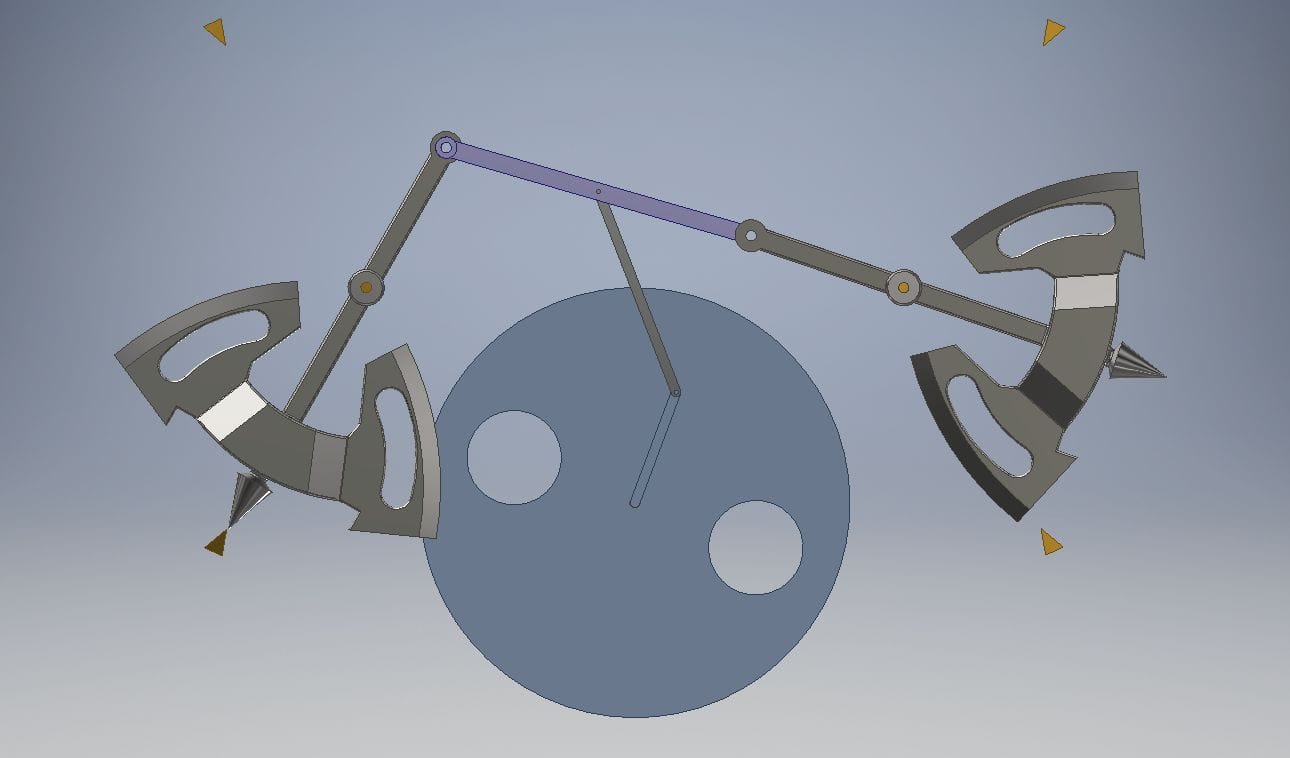
Система простая, симметричная, но презабавнейшая – состоит из двух одинаковых балансиров, соединенных тягой. Разумеется, проще показать на рисунке:
Да, балансиры больше похожи на боевые топоры каких-нибудь норманнов-берсерков, но это просто образ: система сразу наводит на мысль и о часовых маятниках, а они, часы, безжалостно отсекают прожитые мгновения нашей жизни. Так сложился образ. Потом, много позже эта же система естественным образом трансформировалась в некий часовой механизм в более привычном виде. Но сейчас не об этом.
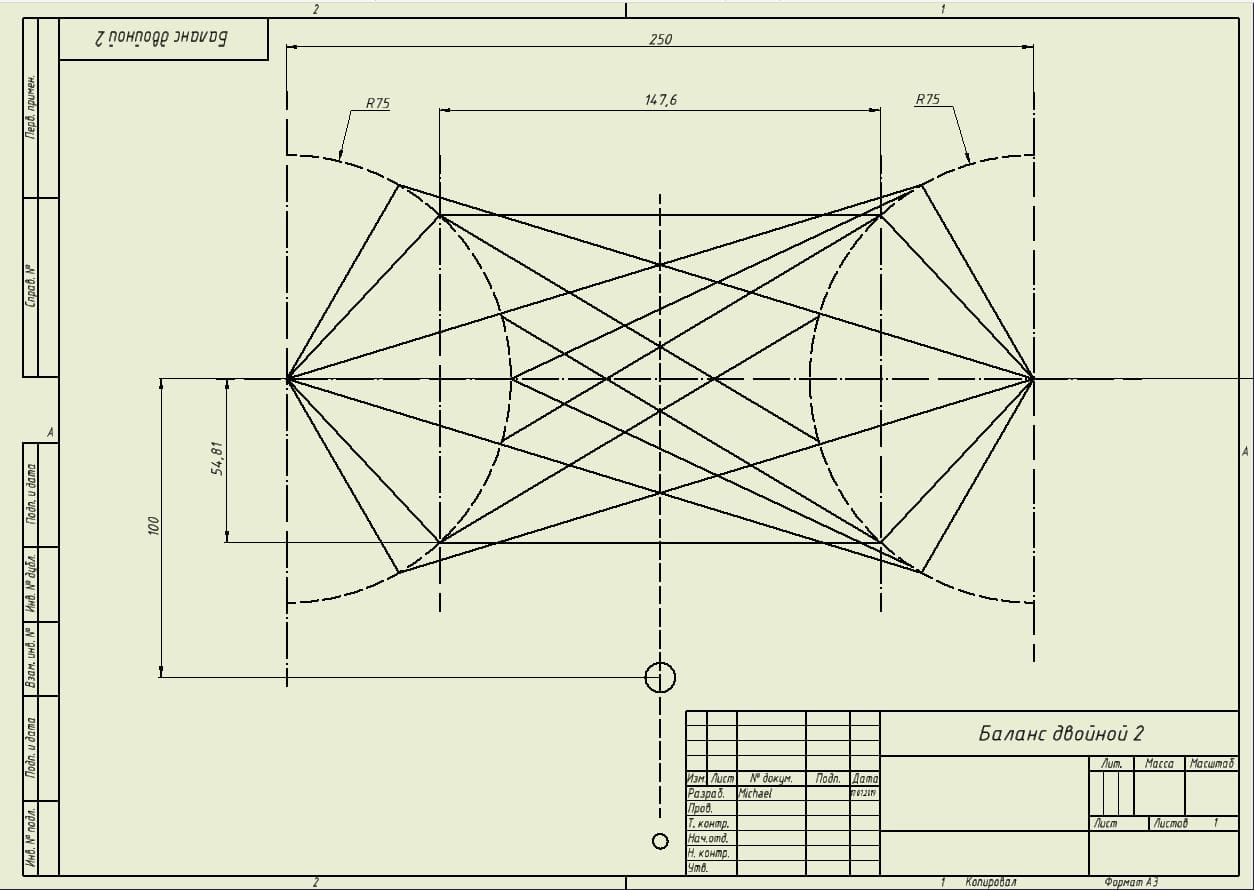
Из рисунка видно, что точки подвеса топоров-балансиров, их оси вращения – неподвижны. Геометрия системы может варьироваться в очень широких пределах, значения длин и радиусов могут составлять хоть десятки метров, хоть миллиметры, а их соотношения также могут сильно отличаться от конструкции к конструкции так, что реализация конструкции может быть очень неожиданной, но схема видна из этого чертежа:
Думаю, что в подробных объяснениях чертеж не нуждается – достаточно сопоставить его с рисунком выше.
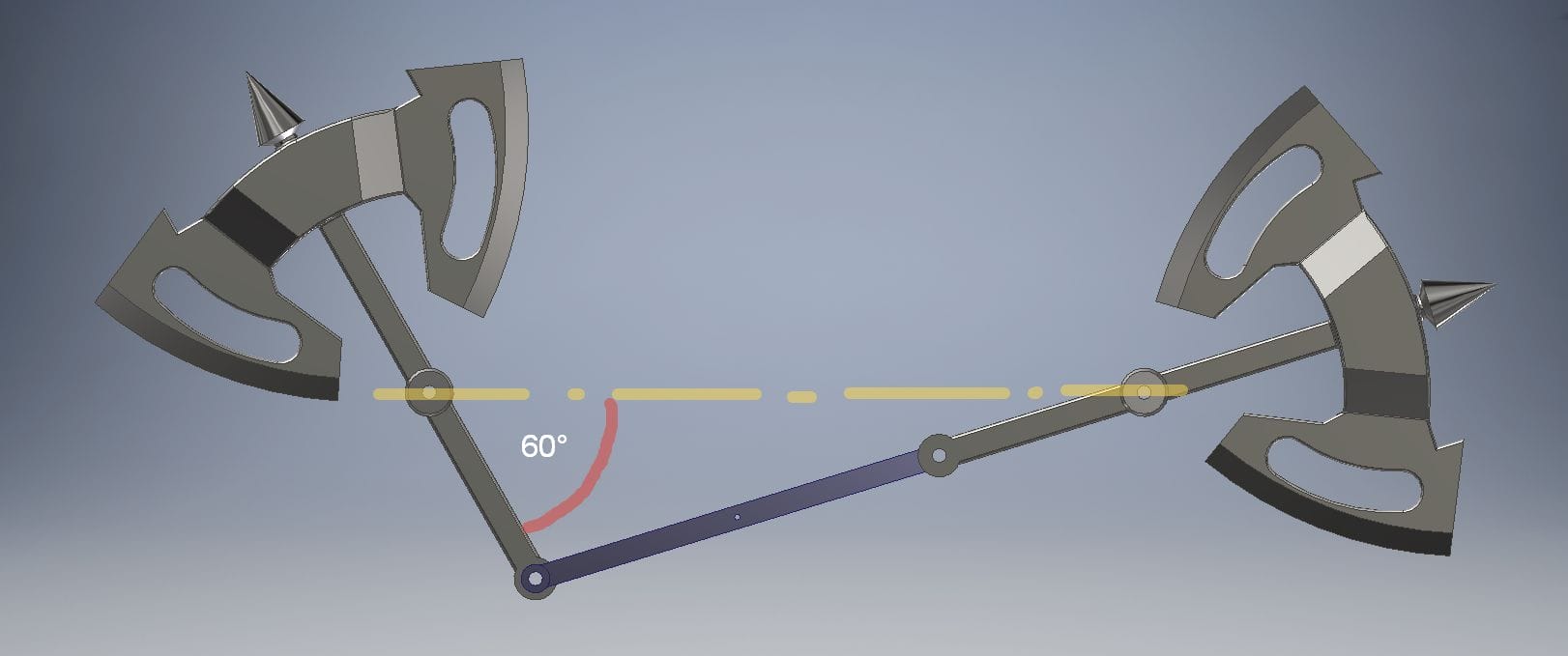
Самое интересное, что в тот самый момент, когда один из «топоров» на максимальной скорости, набрав максимальную кинетическую энергию, вдруг, вынужден остановиться, когда второй «топор» только разогнался и вместе с тягой выстраиваются в прямую линию, длина которой и ограничивает ход первого «топора». Ход второго «топора» ещё не ограничен и он, всю накопленную кинетическую энергию начинает отдавать первому «топору», принуждая его двигаться в противоположном первоначальному направлении. Эта ситуация и изображена ниже:
Левый «топор» более не может двигаться по часовой стрелке – он уже отклонился на предельные в данном случае 60°. Правый же продолжает движение по часовой стрелке и посредством тяги принуждает левый «топор» начать движение уже против часовой стрелки.
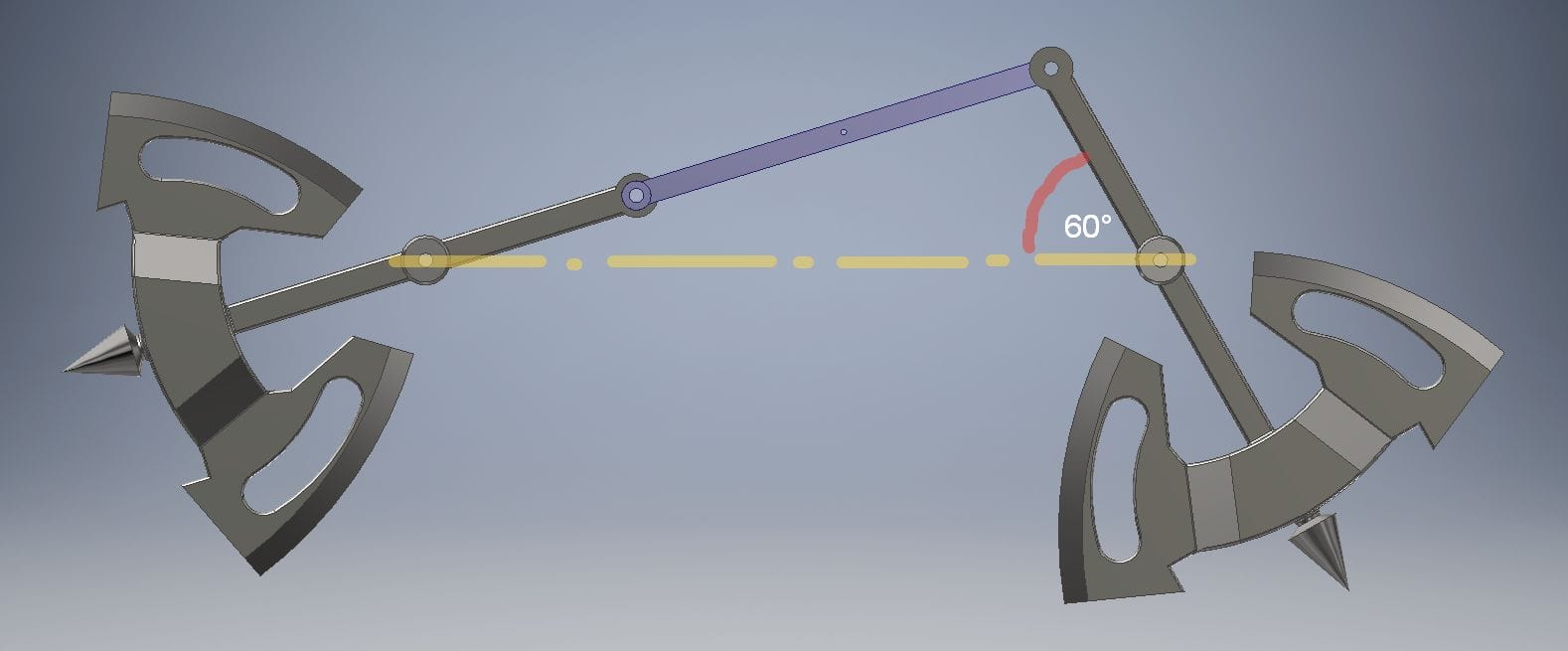
Далее цикл продолжается:
Теперь уже правый «топор» отклонился на свои предельные в данном случае 60° и вынужден резко остановиться и «ждать», когда левый «топор», несущийся против часовой стрелки, вынудит и его к движению против часовой стрелки.
Всё крайне просто, циклично. Варьируя длины, легко получить предельные углы отклонения топоров-балансиров в очень широких пределах.
Важно то, что такая система, очевидно, обладает какой-то своей резонансной частотой, зависящей от моментов инерции всех «участников» движения.
Может быть, кто-то из читателей, найдёт изящное математическое описание динамики этой забавной системы. Мне пока некогда.
Явление лемнискаты народу
А теперь самое время вспомнить о трении: бесконечного обмена энергией не будет из-за трения и нужно сообразить, куда и как подвести к системе подпитывающую энергию, чтобы циклы не затухали.
Куда… Первый «кандидат» в точки подвода – центр симметричной тяги, соединяющей балансиры.
Как… Учитывая цикличность системы, просится кривошип с шатуном. Как-то так, как показано ниже (без излишних пояснений ясно, что где расположено и что с чем соединено, включая маховик, роль которого не так очевидна, и базовые индикаторы – золотистые, всегда неподвижные треугольнички, олицетворяющие систему отсчёта):
Хотите верьте, хотите нет, но у меня с самого начала закралась мысль о том, что центральная точка тяги должна описывать какую-то знакомую из математики замкнутую кривую. И, скорее всего, это должна быть лемниската Бернулли или нечто, очень на нее похожее, близкое к ней. Но как это доказать?
Есть для таких целей в Inventor во вкладке Среды → Динамическое моделирование инструмент Трассировка. Инструмент несколько капризный, но очень полезный.
В окне Динамическое моделирование жмём значок Устройство графического вывода:
Стрелками я достаточно подробно показал, что оси кривошипа нужно задать крутящий момент, увеличить время симуляции с одной секунды по умолчанию, до нужного значения, выбрать пункт Трассировка, там выбрать систему отсчёта и деталь, траектория точки которой нас интересует, указать эту точку, задать цвет графика выводимой траектории и, наконец, запустить Симулятор и получить загадку:
На первый взгляд всё нормально: на графике видно, что сделано пять оборотов кривошипа с возрастающей, как и положено, угловой скоростью. Но получилась только половина траектории (зеленая линия), половина кривой, похожей на лемнискату и сколько бы оборотов не сделал кривошип – центральная точка тяги при симуляции на мониторе описывает только половину графика, как бы я не менял геометрию, крутящий момент и другие параметры, а я перепробовал много вариантов. Но так быть физически не должно. Кривая обязана быть замкнутой и симметричной!
Может быть, сказывается известное коварство т. н. «точки разрыва» – математика не любит такие точки, а лемниската содержит таковую и математическое ядро программы просто «путается»… Загадка.
По непонятной мне причине балансиры как бы натыкаются на невидимую преграду, отскакивают, и симметрия не соблюдается, что мы и видим:
Поиски отгадки
Первое, что приходит на ум – в симуляции не хватает каких-то сил или сила тяжести, а она там есть по умолчанию, направлена «не так».
Вторая мысль похитрее – нужно так модифицировать точку приложения – поднять ее выше или ниже, чтобы создать дополнительный «рычаг» и, тем самым, внести дополнительный крутящий момент для тяги, значимый для программы.
Модифицируем тягу – на рисунке она теперь зеленая и Т-образная:
Однако, вопреки ожиданиям, на Inventor такое существенное с физической точки зрения действие, как перенос точки приложения силы, не произвело никакого «впечатления» и трассировка осталась прежней, половинчатой.
Ещё загадочнее стало. Реальная, физическая система не могла бы проигнорировать такую модификацию.
Тупичок
Хорошо. Но это ещё не конец. Можно ещё попробовать мощный фактор инерции и для этого ещё раз изменим тягу так, чтобы достаточно «увесистая» масса вынудила бы Inventor вспомнить реалии:
Согласен, теперь тяга с «довеском-молотком» выглядит пугающе, некрасиво, но ради результата пойдешь и не на такие издержки.
Однако, и эта «наихитрейшая» хитрость не помогла. И как преодолеть это препятствие, как квалифицировать, на что «списать» – это мой творческий тупик или предел возможностей симулятора программы?
Было бы здорово прокрутить все описанное реально, в «железе». Вдруг, у кого-то из читателей возникнет такое желание и такая возможность.
Спуск
Не хочется обрывать поэму о двух топорах на неопределенности. Тем более, что эта система так и просится послужить часовому делу, а кривошип в таком случае будет носить гордое название – спуск.
Мне известны всего две-три конструкции спуска, из которых самая известная – анкерная.
Вот и еще загадка: может ли мой забавный механизм стать полноценным часовым спуском или так и останется курьезом.
При возможности постараюсь рассказать и о таком воплощении системы балансиров и тяги, но уже в другой раз.
Подводные камни динамического моделирования
Мне очень нравится «Динамическое моделирование». Благодаря этому инструменту можно узнать много интересного и нового про задуманный механизм.
Но следует пользоваться им крайне аккуратно и осмотрительно.
Дело в том, что симуляция – процесс длительный, в результате которого программа создает временные файлы тем большие по размеру, чем больше секунд мы отводим процессу.
Для наших не суперкомпьютеров создается буквально стрессовая ситуация, когда «подкачиваются» сотни и тысячи кадров с визуализацией работы нашего механизма.
И при этом часто возникает ложное впечатление, что компьютер «завис», а он просто обрабатывает огромную очередь операций и изображений.
Крайне важно не торопить машину и не обрывать процесс. Обязательно нужно дождаться момента, когда станет очевидно, что комп снова реагирует на наши команды, что меню снова откликается на перемещения курсора.
Будет совсем хорошо, если перед новым сеансом динамического моделирования, мы педантично выйдем из этого режима по соответствующей кнопке меню.
Если же гнать машину без оглядки, обрывать как попало один сеанс и начинать второй, третий и т. д., то можно получить такой жестокий «краш», что мало не покажется – придётся переустанавливать Inventor и не его одного.
Увы, я сам торопыга и лихой «наездник» на «железе» – дописываю эту заметку по результатам своего личного опыта.