У попередніх розділах обговорювалися прийоми побудови креслень в площині XY. Положення будь-якої точки в цій системі координат характеризується двома значеннями – абсцисою і ординатом. Для виконання конструкцій в тривимірному просторі до цих координат додається третє значення, яке визначає обсяг конкретного виробу. Йдеться про координату Z, яка надає плоским об’єктам обсяг. Уміння правильно задавати координати тривимірних об’єктів сприяє правильному моделюванню просторових деталей. Для цього AutoCAD має три типи систем відліку: тривимірні декартові, циліндричні і сферичні координати.
ДЕКАРТОВІ КООРДИНАТИ
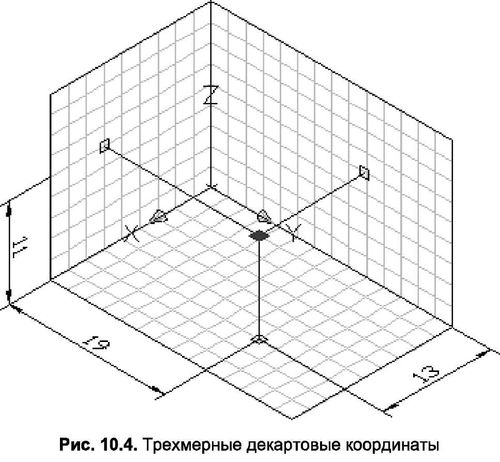
Для позначення положення точки в тривимірному просторі за допомогою декартових координат необхідно додати до значень її координат на площині XY третє значення – координату Z. На рисунку 10.4 показана точка, де координати в площині XY – 13, 19, а координати осі z – 11 одиниць.
При введенні координат в цю систему спочатку задається координата X, потім розділяється комою Y, а вже потім Z. Наприклад: 13,19,11. Якщо числове значення координати дробове, то необхідно відокремити цілочисельну і дробову частини точкою. Крім того, не допускаються пробіли між числами і комами.
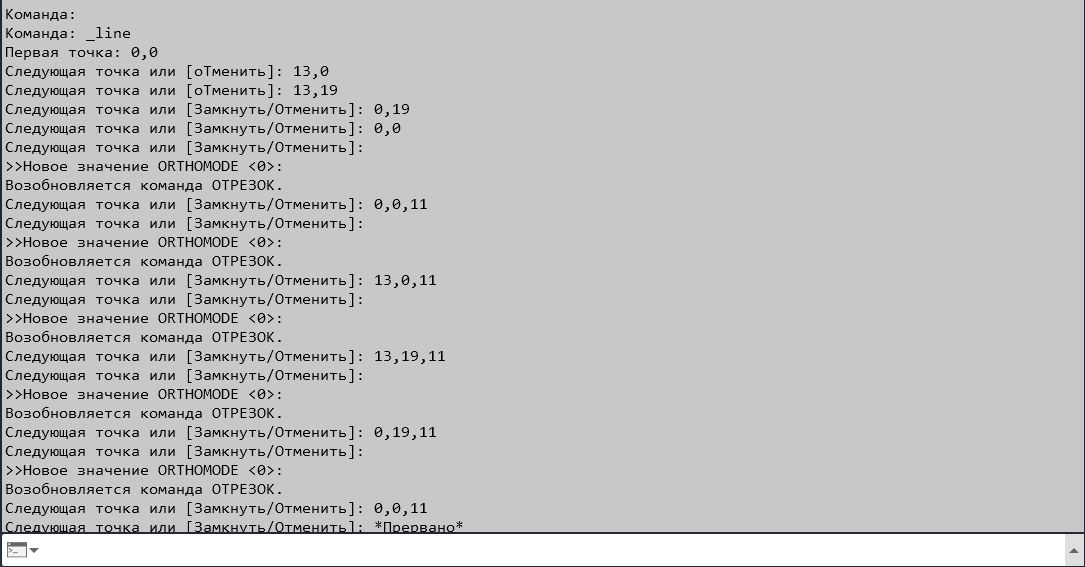
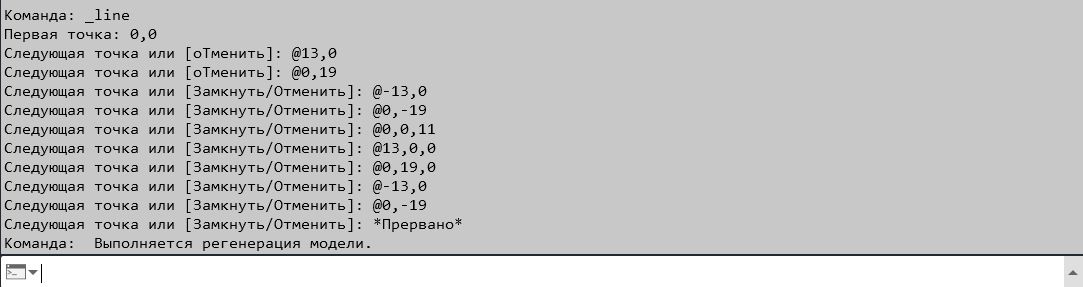
Спробуємо побудувати паралелепіпед з ліній, з розмірами 13,19,11, використовуючи тривимірну систему координат. Для цього в головному меню вибираємо Сегмент. Щоб встановити вихідну точку паралелепіпеда в координатах (0,0,0), використовують динамічний вхід. Після вибору параметра Сегмент введіть 0.0 Enter. Ви можете використовувати клавішу табуляції замість “, у динамічному введенні. AutoCAD використовує абсолютні і відносні координати. У разі абсолютних координат посилання робиться від початку координат, а відносні координати підраховуються від останньої заданої точки і позначаються знаком @, абсолютні координати – знаком # перед введенням координат. Спробуємо провести паралелепіпед, використовуючи вхід координат.
Ми отримали недобудований паралелепіпед, для завершення будівництва можна вручну намалювати 3 відсутніх лінії.
Приклад введення абсолютних координат для побудови паралелепіпеда.
Приклад введення відносних координат для побудови паралелепіпеда.
Після додавання відсутніх ліній і розмірів. Як бачите, вийшло так, як потрібно.
Примітка. Якщо ви пропустите значення Z при введенні координат в тривимірному просторі, AutoCAD автоматично присвоїть йому значення за замовчуванням, записане в змінній системи ELEVATION, яка називається висотою.
При створенні тривимірних об’єктів використовуються поняття висоти (рівня площини XY) і висоти. Висота визначається Z-координатою площини XY, на якій побудований об’єкт. Зрозуміло, що якщо висота дорівнює нулю (значення за замовчуванням), то рівень об’єкта (його площина) збігається з площиною XY. При позитивному підвищенні об’єкт знаходиться над площиною XY, а при негативному підвищенні – нижче. Що стосується висоти тривимірних об’єктів, то вона визначає відстань, на яке зміщується об’єкт щодо висоти.
Зазвичай до редагування параметрів висоти і висоти вдаються в тому випадку, коли необхідно побудувати кілька точок, в яких координата Z має однакове значення. Спрощення конструкцій викликано тим, що досить буде ввести тільки два значення для кожної такої точки, які визначають її положення в площині XY.
Як зазначалося, поточне значення висоти зберігається як змінна системи ELEVATION, а висота як змінна THICKNEES. Для того щоб змінити значення обох параметрів, присвоєних новоствореним об’єктам, потрібно запустити команду Елева і відповісти на наступні питання:
Командування: Єлев
Вкажіть нове значення висоти <за замовчуванням 0,0000>: <введення нового значення висоти>
Вкажіть нову товщину <за замовчуванням 0,0000>: <введіть нове значення висоти>
Також слід зазначити, що висоту об’єкта можна змінювати з палітри Properties.
ЦИЛІНДРИЧНІ КООРДИНАТИ
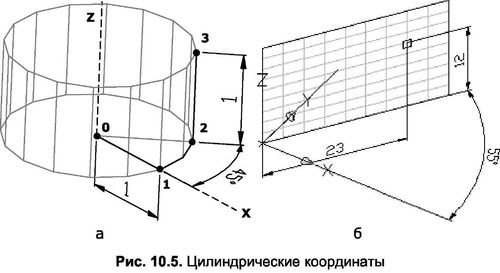
Положення точки в циліндричних координатах також визначається трьома величинами, але одна з них незграбна.
Як відомо, круговий циліндр утворюється при обертанні утворюючого 2-3 (рис. 10,5а) навколо кола, що описує кут в 360 °. Саме цей принцип втілюється в понятті циліндричних координат. Визначаючи положення точки, необхідно задати спочатку радіус циліндра (0-1), потім кут повороту формує (1-2) і, нарешті, висоту циліндра (2-3). Так, наприклад, точка, зображена на рис. 10.36, був побудований щодо діючої УКС після введення 23<55,12 в командному рядку. Ікона «
Слід звернути увагу на правило ознак. Що стосується лінійних координат, то тут все просто – напрямок осей визначає додатні значення еталона. При цьому позитивним напрямком осі Z можна керувати за правилом правої руки. Правило полягає в наступному. Якщо великий палець правої руки вирівняний з віссю х, а вказівний – з віссю y, то решта пальців в вигнутому положенні будуть вказувати на позитивний напрямок осі z (рис. 10.56).
Щоб визначити позитивний напрямок обертання щодо будь-якої осі, потрібно дотримуватися наступного правила. Якщо встановити спостерігача з позитивного напрямку осі, то позитивний напрямок кутового орієнтира буде збігатися з рухом проти годинникової стрілки (рис. 10.4). Тому для введення напрямку кута за годинниковою стрілкою необхідно ввести значення кута зі знаком мінус.
Наприклад, давайте побудуємо циліндр з декількома отворами, розташованими під різними кутами. Для початку створимо осі майбутніх отворів, ввівши координати. Нижче наведено приклад введення абсолютних і відносних циліндричних координат.
Для створення осей отворів скористаємося наступними координатами:
0,0,10
25<0,8
0,0,35
25<45,10
Давайте пропустимо наступні конструкції з використанням ПСК і віднімання твердих тіл, так як вони будуть розглянуті на інших уроках і побачить результат, який виходить в результаті.
СФЕРИЧНІ КООРДИНАТИ
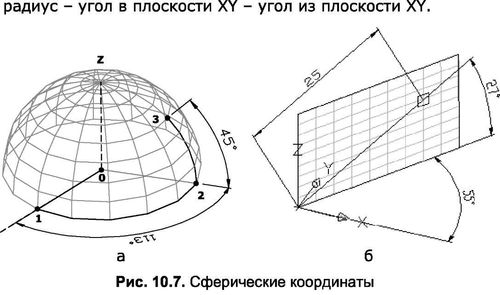
Положення точки в сферичних координатах також визначається трьома величинами, з яких одна є лінійною, а дві інші – кутовими.
Як відомо, сферична поверхня – це геометричне місце точок в просторі рівновіддалене від однієї точки – центру кулі. Тому для того, щоб визначити положення точки, розташованої на поверхні сфери (рис. 10.7а), досить вказати радіус кола, обертанням якого утворюється куля (0-1), потім кут, утворений поворотом кола навколо осі Z (1-2), і, нарешті, кут, утворений поворотом кола щодо осі х (2-3). Так, наприклад, точка, зображена на рис. 10.76, був побудований щодо поточного UCS після набору 25<55<27 в командному рядку. Ікона «
Сферичні координати, як і попередній приклад, можуть використовуватися для додаткових конструкцій на опуклих і увігнутих поверхнях.
ТОЧКОВІ ФІЛЬТРИ
Координатні точкові фільтри – це ще один спосіб введення координат в тривимірному просторі, відмінною рисою якого є залежність від координат раніше введених об’єктів. Іншими словами, щоб призначити координати таким способом, потрібно прив’язати до вузлів вже існуючих об’єктів, щоб автоматично витягти з них замовлені вами координати.
Примітка. Установка координат в тривимірному просторі шляхом фільтрації точок може бути ефективною тільки при використанні режимів відліку об’єкта.