Для виконання точних конструкцій можна використовувати безліч різних інструментів і режимів побудови, але починати їх вивчення слід, на думку авторів, методом безпосередньо введення координат точки в командний рядок. AutoCAD 2010 використовує кілька систем координат. Розглянемо ті з них, які відносяться до двовимірних систем координат, т. Е. Декартова і полярна системи.
ДЕКАРТОВИЙ РЕЖИМ
У декартовій системі координати будь-якої точки на площині визначаються її положенням щодо точки перетину двох взаємно перпендикулярних осей X і Y. Ця точка називається початком координат. У цьому випадку положення будь-якої точки на площині характеризується двома значеннями: перша –абсцисою точки точки, тобто. відстань від початку координат до проекції цієї точки на осі x, а потім ординат цієї точки вводиться через кому – відстань від початку координат до проекції точки на осі Y. Координати вважаються позитивними, якщо на осі абсциси вони відкладаються вправо, а на осі ординат вгору.
Приклад 3.1
Використання декартової системи координат
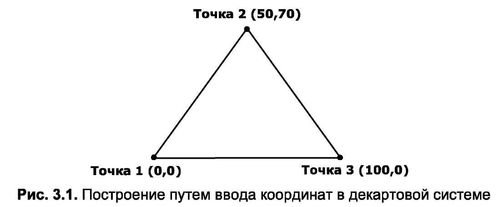
Цей приклад демонструє побудову фігури (рис. 3.1), використовуючи декартову систему координат.
Для виконання точних конструкцій можна використовувати безліч різних інструментів і режимів побудови, але починати їх вивчення слід, на думку авторів, методом безпосередньо введення координат точки в командний рядок. AutoCAD 2010 використовує кілька систем координат. Розглянемо ті з них, які відносяться до двовимірних систем координат, т. Е. Декартова і полярна системи.
ДЕКАРТОВИЙ РЕЖИМ
У декартовій системі координати будь-якої точки на площині визначаються її положенням щодо точки перетину двох взаємно перпендикулярних осей X і Y. Ця точка називається початком координат. У цьому випадку положення будь-якої точки на площині характеризується двома значеннями: перша –абсцисою точки точки, тобто. відстань від початку координат до проекції цієї точки на осі x, а потім ординат цієї точки вводиться через кому – відстань від початку координат до проекції точки на осі Y. Координати вважаються позитивними, якщо на осі абсциси вони відкладаються вправо, а на осі ординат вгору.
Приклад 3.1
Використання декартової системи координат
- Цей приклад демонструє побудову фігури (рис. 3.1), використовуючи декартову систему координат.
Лінія, розташована у групі знарядь “Креслення” на вкладці “Примітка”. - Коли з’явиться запит на першу точку, введіть її координати (0,0) і натисніть Клавішу Enter.
- Коли з’явиться запит Вкажіть наступну точку або [Undo] введіть координати другої точки (50.70) і натисніть Enter. У цей момент ви також можете використовувати параметр Скасувати, ввівши його скорочене ім’я U в командному рядку.
- У відповідь на аналогічне питання повинні бути вказані координати третього пункту (100, 0). Якщо в цей момент ввести скорочене ім’я (U) параметра Undo, координати другої точки будуть невписані.
- Коли з’явиться запит на координати четвертої точки, введіть 0,0 або C (параметр Close) і двічі натисніть Enter (вдруге необхідно натиснути клавішу Enter, щоб закінчити роботу з командою Line).
Перелік коду 3.1
Побудова трикутника з використанням декартової системи координат
Команда: Рядок Вкажіть першу точку: 0,0
Вкажіть наступний пункт або [Undo]: 50,70
Вкажіть наступну точку або [Undo]: 100,0
Вкажіть наступну точку або [Close/Undo]: 0,0
Вкажіть наступну точку або [Undo]: J
ПОЛЯРНИЙ РЕЖИМ
Цей режим малювання заснований на використанні полярної системи координат. В даному випадку координати точки визначаються двома параметрами: перший – відстань від витоку; другий – кут між нульовим напрямком полярної системи відліку і вектором, спрямованим від початку координат до вхідної точки (напрямного вектора).
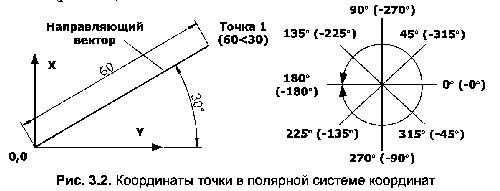
Синтаксис полярної системи координат виглядає наступним чином: [X<y></y>, где X – значение расстояния; Y – значение угла. Как и в синтаксисе декартовых координат, все данные вводятся без пробелов между переменными и знаком «<encoded_tag_open />» угла. Например, для того чтобы обозначить точку (точка 1), направляющий вектор которой образует с нулевым направлением полярной системы координат угол 30° и которая удалена от центра координат на 60 единиц, следует ввести такую строку: 60<encoded_tag_open />30 (рис. 3.2). <a href= https:=””]
Примітка. У полярній системі координат за замовчуванням зворотний напрямок позитивного кута збігається з напрямком проти годинникової стрілки, і навпаки – зворотний напрямок негативного кута за замовчуванням збігається з напрямком за годинниковою стрілкою (рис. 3.2).
Приклад 3.2
Використання полярної системи координат
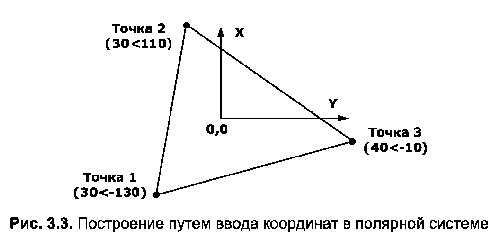
Цей приклад демонструє побудову фігури (рис. 3.3) за допомогою полярної системи координат.
Порядок виконання роботи наступний (Перерахування 3.2).
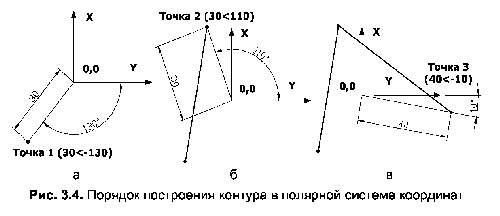
- Будь-яким відомим способом виконайте команду Line, введіть на першому запиті полярні координати першої точки, рівні 30-130< (рис. 3.4а), і натисніть Enter.
Примітка. Якщо ввести негативну кутову координату, наступна точка буде побудована шляхом обертання напрямного вектора за годинниковою стрілкою, а якщо лінійна координата стане від’ємною, точка почне будуватися в напрямку, протилежному напрямку кутового вектора. - У відповідь на питання Вкажіть наступний пункт або [Undo] потрібно ввести координати другої точки (30<110), і натисніть Enter. Як малюнок. 3.46, координати другої точки рахуються не з попереднього пункту, а від початку координат.
- У відповідь на аналогічне питання вводяться полярні координати третьої точки (40-10<): операція завершується натисканням клавіші Enter (рис. 3.4с).
- Коли з’явиться запит на отримання координат четвертої точки, введіть C (параметр Close), щоб утворити шлях, і натисніть Enter.
Перелік коду 3.2
Побудова трикутника за допомогою полярної системи координат
Команда: Рядок Вкажіть першу точку: 30-130<
Вкажіть наступний пункт або [Undo]: 30<110
Вкажіть наступну точку або [Undo]: 40-10<
Вкажіть наступну точку або [Close/Undo]: С
Вкажіть наступну точку або [Undo]: J
ВІДНОСНІ КООРДИНАТИ
[ads]
Наведені вище приклади побудови в різних системах координат демонструють можливості введення абсолютних значень вершин – точок, відрахованих від походження. Цей прийом не завжди зручний і тому в більшості випадків при розробці креслення використовуються відносні координати точок. Згідно з цим режимом, координати останньої введеної точки, тобто координати останньої вхідної точки, беруться за відправну точку. початок координат «переноситься» в точку, яка була введена на попередньому етапі побудови або редагування об’єкта, і з нього буде розрахована наступна координата.
Примітка. Використовуючи певний синтаксис, у відносні координати можуть бути введені як декартові, так і полярні координати, звані відносними декартовими і відносними полярними координатами відповідно.
Відносний синтаксис координат декартової координати – це два значення (X і Y), які враховуються з попередньої точки. При цьому обов’язковим атрибутом таких координат повинен бути знак @, введений перед основними значеннями без пробілу (наприклад: @40,-50).
Використання відносних декартових координат особливо корисно при побудові креслярських елементів, що складаються з лінійних ознак, паралельних осям X і Y. Ортогональна. Що стосується відносних полярних координат, то слід зазначити, що вони мають набагато більше застосування на практиці, ніж абсолютні координати, і зручні в тих випадках, коли відома відстань і кут, що утворюються між базовим вектором і напрямною.
Нижче наведено ряд прикладів, які починаються з демонстрації конструкції з використанням відносних декартових координат. Застосування цієї методики можливо тільки в тому випадку, якщо відома координатна прив’язка наступної точки щодо попередньої.
Приклад 3.3
Використання відносних декартових координат
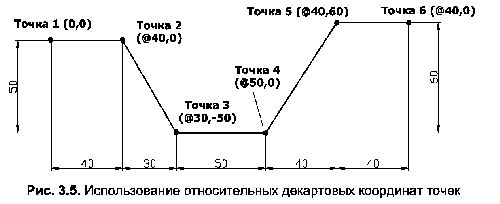
Цей приклад демонструє особливості побудови зображеного на рис. 3,5 фігури у відносних декартових координатах.
Порядок виконання роботи наступний (Перерахування 3.3).
- Будь-яким відомим способом запустіть команду Line, введіть 0.0, коли з’явиться запит на координати першої точки, і натисніть Enter.
- Коли з’явиться запит на наявність координат другої точки, введіть @40.0 і натисніть клавішу Enter. Зазначення значка @вказує на використання відносних координат – координат, відрахованих від раніше введеної точки (0,0).
- Коли з’явиться запит на координати третьої точки, введіть @30,-50 і натисніть клавішу Enter.
- При запиті на координати четвертого і п’ятого пунктів введіть @50.0 і @40.60 відповідно.
- Коли з’явиться запит на наявність координат останнього, шостого пункту, введіть @40.0 і двічі натисніть клавішу Enter.
Перелік коду 3.3
Будівництво котловану у відносних декартових координатах
Команда: Рядок Вкажіть першу точку: 0,0
Вкажіть наступну точку або [Undo]: @40,0
Вкажіть наступну точку або [Undo]: @30,-50
Вкажіть наступну точку або [Close/Undo]: @50,0
Вкажіть наступну точку або [Close/Undo]: @40,60
Вкажіть наступну точку або [Close/Undo]: @40,0
Вкажіть наступну точку або [Undo]: J
Відносні полярні координати, як і відносні декартові координати, використовуються на практиці набагато частіше, ніж їх «абсолютні» аналоги. Справа в тому, що в більшості випадків забудовник знає відстань (або координату). X) і кут (або координата) Y) які визначають положення наступної точки щодо попередньої точки, а не щодо походження. Останнє робить відносні координати більш популярними.
Примітка. У той момент, коли команда підкаже вам ввести координати точки, ви можете ввести тільки символ @ (без координат) і натиснути Enter, після чого AutoCAD «запам’ятає» координату останньої введеної точки і почне будуватися не з центру координат, а з нього.
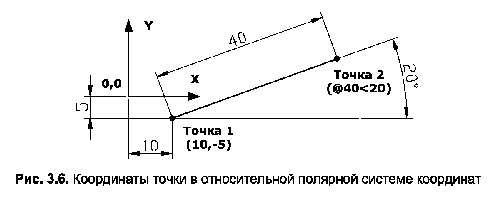
Введення відносних полярних координат, як і декартових координат, також починається з символу І це єдина відмінність між полярним вхідним синтаксисом і абсолютними полярними координатами. Наприклад, для того щоб намалювати відрізок (рис. 3.6), вихідна точка якого вже відома (точка 1), а також довжину відрізка (40 одиниць) і кут його нахилу (20°), досить запустити команду Line, вказати на першому натяку прив’язку до точки 1, а потім ввести в командному рядку: @40<20.
ОРТОГОНАЛЬНИЙ РЕЖИМ
Розглянемо особливий випадок відносних полярних координат, який полягає в тому, що AutoCAD автоматично визначає напрямок лінії, що будується в залежності від заданого користувачем положення курсора. Такий спосіб побудови зручний з точки зору часу, заощадженого при малюванні, так як значно скорочує введення даних, необхідних для побудови координат. Такий спосіб побудови в певному сенсі можна назвати методом «напрямок-відстань», але на відміну від останнього способу, він працює в зв’язці з режимом Ortho Mode, який дозволяє малювати строго горизонтальні або вертикальні лінії.
ОБ’ЄДНАННЯ РЕЖИМІВ ВВЕДЕННЯ КООРДИНАТ
Далі розглядається найбільш поширений метод побудови, заснований на поєднанні вищеописаних режимів введення координат точок, – комбінований. Суть цього методу полягає в тому, що користувач самостійно вибирає найбільш зручний або просто єдино можливий формат координат для кожної точки креслення. Це можуть бути як відносні, так і абсолютні координати.
Приклад 3.4
Використання комбінованого методу
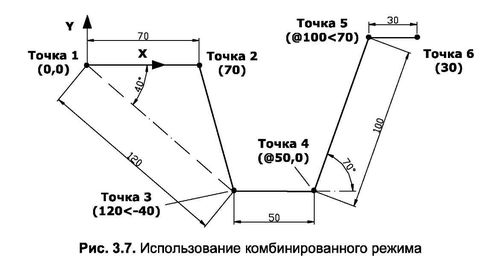
У цьому прикладі описується побудова малюнка, показаного на рис. 3.7. рисунки комбінованим методом.
Порядок виконання роботи наступний (Перерахування 3.4).
- Виконайте команду Line, введіть 0.0, коли з’явиться запит на координати першої точки, і натисніть Enter.
- Переконайтеся, що режим орто ввімкнуто.
- Коли з’явиться запит на координати другої точки, введіть 70 і натисніть Enter, навівши курсор праворуч від початку координат. Слід зазначити, що координати другої точки вводяться за допомогою методу «напрямок-відстань».
- При підказці координат третьої точки введіть 120 -40 <і натисніть Enter (координати третьої точки були введені за допомогою полярних координат).
- Коли з’явиться запит на координати четвертої точки, введіть @50.0 і натисніть Enter (координати вводяться за допомогою відносних декартових координат).
- Коли з’явиться запит на координати п’ятої точки, введіть @100<70 і натисніть Enter (координати вводяться за допомогою відносних полярних координат).
- Коли з’явиться запит на координати шостої точки, досить ввести 30 і двічі натиснути Enter, попередньо навівши курсор миші праворуч від попередньої точки. Він також використовує метод відстані напрямку та режим орто.
Перелік кодів 3.4
Побудова фігури за допомогою комбінованого методу
Команда: Рядок
Вкажіть перший пункт: <Орто на> 0,0
Вкажіть наступний пункт або [Undo]: 70
Вкажіть наступну точку або [Undo]: 120-40<
Вкажіть наступну точку або [Close/Undo]: @50,0
Вкажіть наступний пункт або [Close/Undo]: @ 100<70
Вкажіть наступну точку або [Close/Undo]: 30
Вкажіть наступну точку або [Undo]: J